Archive of Biochemistry
Negative entropy production in L-lactate dehydrogenase kinetics
AV Stepanov1* and MA Stepanov2*
2Department of Technical Physics. Information Technologies and Robotics Faculty, Belarusian National Technical University, B. Khmelnitsky str. 9, Building 11, 220013 Minsk, Belarus
Cite this as
Stepanov AV, Stepanov MA (2023) Negative entropy production in L-lactate dehydrogenase kinetics. Arch Biochem 6(1): 001-009. DOI: 10.17352/ab.000007Copyright License
© 2023 Stepanov AV, et al. This is an open-access article distributed under the terms of the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original author and source are credited.Fröhlich theory of coherent excitations in biological systems is analyzed. L-lactate dehydrogenase kinetics is studied using the activation process model for non-equilibrium cases. The model explains the process of energy accumulation necessary for carrying out catalytic reactions in a living cell by means of interaction of quantum subsystems with thermal equilibrium radiation, light, and radiation energy of metabolic processes occurring in the cell. It is shown that lactate dehydrogenase catalyzes the interconversion of pyruvate and lactate with concomitant interconversion of NADH and NAD+ in three ways, that is, three reactions occur simultaneously. Negative information entropy for the reactions under consideration is calculated. Its absolute value is equal to that of information entropy of the elementary activation act. This fact ensures the principle of stable non-equilibrium and indicates the reaction under consideration belongs to a living cell.
Introduction
What is the difference between living and non-living systems? Ervin Bauer answered this question in his monograph Theoretical biology [1]. He formulated the universal law of biology, which he called the principle of stable non-equilibrium. The principle says, “All and only living systems are never at equilibrium. At the expense of their free energy they ceaselessly perform work against equilibrium, demanded by the physical and chemical laws appropriate to the actual external conditions”.
Erwin Schrödinger suggested that stable non-equilibrium of a living organism, e.g. a living cell can only be realized when it consumes and produces negative entropy [2]. He clarified, “The awkward expression ‘negative entropy’ can be replaced by a better one: entropy, taken with the negative sign, is itself a measure of order. Thus the device by which an organism maintains itself stationary at a fairly high level of orderliness (= fairly low level of entropy) really consists continually sucking orderliness from its environment”.
Every living cell is a seat of numerous chemical reactions. There are about 105-109 of them per second depending on a cell’s type [3]. The surprising thing is that all these reactions should proceed under non-equilibrium conditions following the above principle. A cell’s environment can deliver both material objects, such as molecules, atoms, or ions, and electromagnetic energy to decrease the cell’s entropy.
It should also be noted the chemical reactions under consideration are catalytic. Regarding a cell as a type of thermodynamic engine there are three points distinguishing the cell from the standard Carnot engine [4]. First, cells contain catalysts (enzymes). Second, the catalysts are synthesized within the cell as a result of catalytic reactions. Third, cell volume growth results from membrane synthesis from nutrient components, facilitated by the catalyst.
This brings up other questions. A living cell is at a temperature just higher than room one. Where does it store energy necessary to perform catalytic reactions at characteristic reaction rates? What is the way to store this energy? Herbert Fröhlich, a German-born British physicist, tried to find the answer to these questions. He proposed a theory of coherent excitations in biological systems known as Fröhlich coherence.
Creation and early development of Fröhlich theory
He conjectured that in living systems certain coherent longitudinal electric modes were strongly excited, and stabilized by deformations arising from non linear effects [5]. This conjecture was stimulated by the extraordinary dielectric properties of cells and of some of the relevant gas molecules in conjecture with the requirement of a non-obvious long-range order (coherence) in systems which are relatively stable but not in all respects in thermal equilibrium. The modes were expected to be in a frequency region between 1012 and 1012 Hz [6]. They were based on the dipolar properties of cell membranes; of certain bonds recurring in giant molecules (such as H bonds) and possibly on pockets of non-localized electrons. It was shown that if energy was supplied above a certain mean rate to such a branch, then a steady state would be reached in which a single mode of this branch was very strongly exited. The supplied energy was thus not completely thermalized but stored in a highly ordered fashion. This order expressed itself in long-range phase correlations; the phenomenon had considerable similarity with the low-temperature condensation of a Bose gas. The proposals discussed in [6] were speculative; Fröhlich underlined the need for experimental establishment of the existence of the coherent vibrations in living systems. His theory was actually the development of Bauer’s idea that any living organism is a mechanically strained molecular structure.
Then he assumed that the model could be applicable to enzyme molecules which would posses metastable exited states in which polar groups were stretched so that the molecule could have a very large dipole moment resembling a ferroelectric case, and in which excitations above this state were partly transformed into coherent vibrational modes [7]. An enzyme molecule so exited would have strong long range interaction with other molecules. This interaction would tend to lift other enzyme molecules into the metastable state, the required energy to be provided from the coherently exited modes. These proposals could be tested in three ways. First, by investigation of the build-up of the reaction rate as a function of the enzyme density. Second, by direct observation of the exited coherent modes using Raman effect. Third, by the detection of increase in the static dielectric constant as a result of the expected large increase in the dipole moment of the enzyme molecules when they were transferred to the metastable state.
Selective long range forces which were always attracted could be obtained if the system was pumped as had been suggested to occur in biological systems through their metabolism. It was shown that the lowest frequency in a band of polarization waves should be very strongly exited [8]. The polarization waves with zero wave number were responsible for long range interaction.
First experimental evidence of the action of coherent millimeter electromagnetic radiation on biological systems was mentioned by Fröhlich in [9]. The observed effects were strongly frequency selective at very low power supply thus indicating resonance effects. The existence of a threshold for the power supply below which no effects were found strongly supported Fröhlich’s earlier theoretical prediction that energy supply above a critical rate would lead to excitation of polar coherent modes in the system in a manner comparable to Bose condensation.
Further investigation of the extraordinary dielectric properties of biological materials and the action of enzymes was carried out in [10]. From very general theoretical considerations it was concluded that many biomolecules should have metastable exited states with very high dipole moment, and should be capable of strongly exited giant dipole vibrations with frequencies near 1011 Hz. It was suggested that the two postulates should be of importance of the action of enzymes, and the high polarization could provide for a lowering of activation energies. Two experimental possibilities to prove the excitation of the highly polar state during enzyme activity were considered: (i) measurement of the dielectric increment during enzymatic activity; (ii) measurement of the electric signal arising from activation of the highly polar state. By that time the existence of low frequency modes in proteins had already been demonstrated experimentally [11]. Fröhlich generalized his theory at the Symposium on “Interdisciplinary Aspects of Modern Physics”, in Parma, Italy, 1976 [12]. He stated, “The great success of molecular biology arises from the discovery of the detailed structure of biomolecules such as DNA and enzymes. No systematic spatial order was found, and it was considered that these molecules do not possess a physical order. Physical order, however, does not express itself in spatial order only.” He explained that many other types of physical order could be imposed on certain systems when they were lifted from their thermal-equilibrium state even they were spatially disordered. One of those types was connected with the existence of macroscopic wave functions, which implied the existence of certain quantum phase correlations over microscopic distances or the existence of coherent states. The above-mentioned concept of macroscopic wave function referred to the whole assembly of particles, i.e. it was a collective property which could not in a simple way be reduced to properties of individual particles.
Biological materials, when they exhibit typical biological properties, must be “fed”, i.e. energy passes through them. This energy may arise from chemical processes, or it may be supplied by the Sun. So it was suggested that biological systems belong to ones in which the supply of energy imposed a characteristic order.
Two models were considered in some detail to explain storage and transport of energy in biological systems. The vibrational model assumed that any system containing charged particles was capable of long-wave electrical vibrations. Such a system needed not be homogeneous. The vibrations were strongly coupled to the surroundings, i.e. a heat bath at temperature T. A main difference from ordinary condensation of a Bose gas in thermal equilibrium was noted. There the ordered (condensed) state was reached by lowering the temperature. In the proposed model, the ordered state was reached by supplying sufficient external energy to the system at room temperature. The high-polarization model predicted the existence of the system’s metastable states with spontaneous polarization.
The two types of excitation could have far-reaching biological consequences. First of all, it was noticed that they required supply of energy, i.e. activation. Both could then lead to forces which had been absent before activation, and to storage and transport of energy. Thus, if the coherently excited vibration represented an oscillating giant dipole, then long-range frequency selective forces could be activated. They may lead to selective transportation of molecules like enzymes and thus initiate a particular trend of chemical events. It was suggested that these properties were an essential feature in the high catalytic power of enzymes. Thus the high internal fields arising from the strongly polarized state could reduce activation energies, while excitation of coherent modes could be used for the transport of energy.
Finally, Fröhlich remarked that in active biological systems experimental evidence for the existence of coherent electric oscillations in the 1011 Hz region would require methods which had not been fully developed at that time.
Further development and experimental verification of Fröhlich theory
In 2009 Fröhlich condensates were classified into three types: weak, strong and coherent ones [13]. It was shown that weak condensates could have profound effects on chemical and enzyme kinetics, and could be produced from biochemical energy or from radio frequency, microwave, or terahertz radiation. On the contrary, strong condensates in which an extremely large amount of energy was channeled into one vibrational mode, and coherent condensates in which this energy was placed in a single quantum state were shown to be extremely fragile and inaccessible in a biological environment.
In 2012 the case of a peculiar complex behavior in open boson system sufficiently away from equilibrium, having relevance in the functioning of information-processing biological and condensed matter systems was considered [14]. This was the so-called Fröhlich-Bose-Einstein condensation, a self-organizing-synergetic dissipative structure, a phenomenon apparently working in biological processes and present in several cases of systems of boson-like quasi-particles in condensed inorganic matter. Emphasis was centered on the quantum-mechanical-statistical irreversible thermodynamics of those open systems, and the informational characteristics of the phenomena.
Three types of Bose-Einstein condensation (BEC) were mentioned. The first type of condensation occurs in fluids in equilibrium at very low temperature. Examples are superfluidity in liquid helium, or systems consisting of atomic alkali gases contained in traps. A second type of BEC is the one of boson-like quasi-particles, that is, those associated to elementary excitations in solids (e.g., phonons, excitons, hybrid excitations, etc.), when in equilibrium at extremely low temperatures. The third type is the case of boson-like quasi-particles (associated to elementary excitations in solids) which are driven out of equilibrium by external perturbative forces. Here the authors of [14] introduced the nomenclature NEFBEC (short for Non-Equilibrium Fröhlich-Bose-Einstein Condensation). Several cases of NEFBEC were listed:
- A first case was the many boson system consisting of polar vibration (LO-phonons) in bio-polymers under dark excitation (metabolic energy pumping) and embedded in a surrounding fluid.
- A second case was the one of acoustic vibration (AC phonons) in biological fluids, involving nonlinear anharmonic interactions and in the presence of pumping sonic waves.
- A third one was that of excitons (electron-hole pairs in semiconductors) interacting with the lattice vibrations and under the action of RF-electromagnetic fields.
- A fourth one was the case of magnons, where the thermal bath was constituted by the phonon system, with which a nonlinear interaction existed, and the magnons were driven arbitrarily out of equilibrium by a source of electromagnetic radio frequency.
- A fifth one consisted in a system of longitudinal acoustic phonons driven away from equilibrium by means of drifting electron excitation (presence of an electric field producing an electron current), which had been related to the creation of the so-called Saser, an acoustic laser device.
- A sixth one involving a system of LO-phonons driven away from equilibrium by means of drifting electron excitation, which displayed a condensation in an off-center small region of the Brillouin zone.
It should be noted that only two first cases of NEFBEC could be assigned to living biological systems.
The first experimental observation of Fröhlich condensation in protein structure was presented in 2015 [15]. To that end, terahertz techniques were combined with a highly sensitive X-ray crystallographic method to visualize low-frequency vibrational modes in the protein structure of hen-egg white lysozyme. It was found that 0.4 THz electromagnetic radiation induced non-thermal changes in electron density. In particular, a local increase of electron density in a long α-helix motif was observed consistent with a subtle longitudinal compression of the helix. The observed electron density changes occurred at a low absorption rate indicating that thermalization of terahertz photons happened on a micro- to milli-second time scale, which was much slower than the expected nanosecond time scale due to damping of delocalized low frequency vibrations. It was shown that the micro- to milli-second lifetime of the vibration could only be explained by Fröhlich condensation.
In [16] the activation of out-of-equilibrium collective oscillations of a protein macromolecule as a classical phonon condensation phenomenon was studied both theoretically and experimentally. An aqueous solution of a model protein, the bovine serum albumin, was considered. Its molecules were driven out of thermal equilibrium state by means of optical pumping through the excitation of some fluorochromes bound to each protein molecule. The optical excitation of these fluorochromes created, on each protein, some “hot points” acting as the epicenters of a so-called “proteinquake” and resulting in an energy transfer to the vibrational part of the protein. By attaching an average number of 5 Alexa488 fluorochromes per protein, a considerable amount of energy could be continuously pumped into each protein by means of an argon laser (wavelength 488 nm). Two different and complementary THz near-field spectroscopic techniques – a plasmonic rectenna and a microwire near-field probe – were used in two different labs to eliminate artifacts. The BSA protein displayed a remarkable absorption feature around 0.314 THz. This experimental outcome was in very good qualitative agreement with the theory, allowing the researchers to identify the observed spectral feature with a collective oscillation of the entire molecule.
A full quantum statistical theory using nonequilibrium equations of motion for the Fröhlich condensate was developed in 2018 [17]. The energy redistribution among vibrational modes with nonlinearity included was shown to be essential for realizing the condensate and the phonon-number distribution, revealing the transition from quasi-thermal to super-Poissonian statistics with the pump. The spectroscopic properties of the condensate were studied, which were especially revealed by the narrow line width. That gave the long-lived coherence and the collective motion of the condensate. It was demonstrated the BSA protein and lysozyme were most likely the candidates for observing such collective modes in THz regime by means of Raman or infrared spectroscopy.
Zheng and Li stated their belief that despite intense investigations, no unambiguous identification of a Fröhlich condensate had been proved [18]. To create it, they realized the effective two-phonon-energy-redistribution processes between different mechanical modes by placing an array of membranes in the middle of an optical cavity so that the interaction between the optical and mechanical mode was proportional to the square of the displacement. By making use of the adiabatic approximation, the optical field could be treated as a controllable reservoir, which was quite different from the biological systems where the two-phonon processes were determined by the environment. The authors suggested that Fröhlich condensates in optomechanical systems had potential applications in generating narrow-linewidth phonon laser. By switching the role of phonon and photon, the Fröhlich-like photon condensate might be realized and used in acoustic-induced-optical lasing.
So, the above-listed experimental data prove the existence of the Fröhlich condensate. However, all the experiments concerning biological systems were conducted
In summary, it should be noted the investigated Fröhlich condensates have only THz resonant frequencies, while those for a living cell fall in the broad range between Hz and PHz [20]. Therefore, it would be unreasonable to reduce the process of energy accumulation necessary for carrying out catalytic reactions in a living cell only to the Fröhlich condensate. Recent advances in computational calculations of quantum interactions in large chemical and biological systems make it possible to study this process by various means [21-23].
A living organism is a complex information-functioning system, and perhaps that is why information entropy should be involved in the study of this phenomenon. Therefore, the purpose of this paper is to justify the validity of the principle of stable non-equilibrium for L-lactate dehydrogenase kinetics. To do this, the value of negative information entropy will be calculated for an elementary activation act using the activation process model.
The activation process model
First of all, it should be noted that this model is of a microphysical order. It describes the elementary act of chemical transformation based on two assumptions:
- In elementary activation interaction act, potential energy of moving atoms changes discretely or in quanta. Elementary activation act appears to be a series of quantum subsystems occurring in sequence. These subsystems can also be defined as identical quantum oscillators.
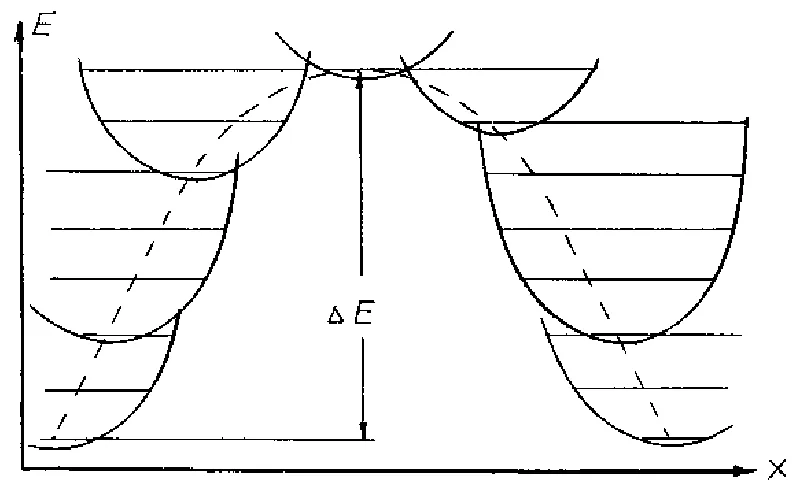
- In statistical equilibrium with thermal radiation an energy exchange between radiation and interacting atoms results in discrete translational motion changes of those atoms which absorb and subsequently emit an oscillation energy quantum series (Figure 1).
With these assumptions in mind, average energy of activation process was calculated as [24,25].
Later the model was developed using the quantum canonical Gibbs distribution. The degeneracy and exclusion of some excited vibrational levels were taken into consideration:
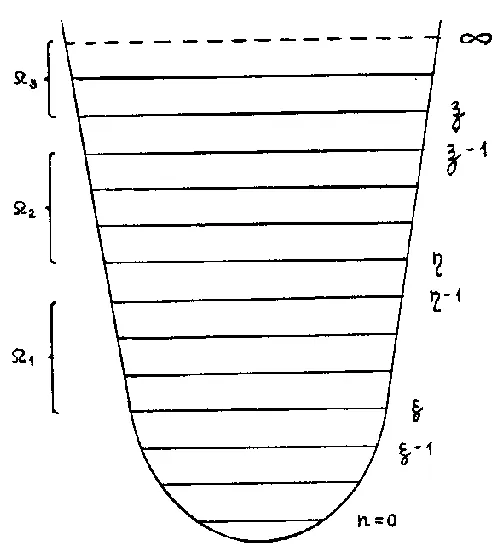
Where Pn expresses the probability that an oscillator has energy equal to nhν and its degree of degeneracy is Ω(nhν).
Then it was presumed that different levels (or groups of levels) in the quantum oscillators can have the different degrees of degeneracy, e.g., Ω1, Ω2, Ω3 (Figure 2), i.e. the vibration levels up to quantum number ξ – 1 are non-degenerate, the ones from quantum numbers ξ to η – 1 have the degeneracy Ω1, and those from η to ζ – 1, Ω2, and from ζ to ∞, Ω3.
Consequently, Eq. (1) was rewritten as [26]:
Where Q=e-mhν/kT, mhtsym
= ΔE is the activation energy, A= Ω1m -1, B= Ω2m - Ω1m, C = Ω3m – Ω2m , D=1-Q-1.
Eq. (2) in its turn was simplified excluding D [27]:
The first term in Eq. (3) is the average energy of activation process for ideal quantum oscillators as described by Eq. (1), whereas the second term accounts for their degree of degeneracy. The main parameter of the model is ν. The value of ν equals to the Einstein spontaneous emission coefficient A [28]. Information entropy for this case can be calculated using the following formula [29]:
These formulas were obtained for the equilibrium case, that is, when a transforming molecule interacts with thermal equilibrium radiation.
Application of the activation process model for non-equilibrium cases
The model was applied to several types of molecules, positive molecular ions, clusters and proteins surrounded by intensive infrared laser radiation [30,31]. Dissociation of SF6 molecules and the C8H8+ ions, self-diffusion processes in Si, Ge, and GaAs clusters, folding and incorporation of β-branch of Escherichia coli membrane protein A (OmpA) into DOPC bilayers were simulated numerically.
To explain IR multiphoton absorption according to the model, its main assumptions were somewhat reformulated:
- As a molecule transforms, its potential energy changes discretely or in quanta. Transformation act appears to be a series of quantum subsystems occurring in sequence. These subsystems can also be defined as identical quantum oscillators.
- An energy exchange between intensive IR radiation and the molecule’s atoms results in discrete translational motion changes of these atoms which absorb quanta of oscillation energy till the molecule’s structure is completely transformed.
Two remarks were made in order to reformulate the assumptions.
First, it was assumed that the number of quantum subsystems m forming a barrier was a constant value, i.e. m was an internal characteristic of the molecule, independent of external conditions. That number did not depend on whether the molecular structure was transformed while interacting with thermal equilibrium radiation or with intensive field of IR laser radiation. Second, the law of conservation of energy was used:
Here is the average energy of elementary act in the Boltzmann-Arrhenius model [25]:
Where ρhν is the activation energy, ρ is the number of equal quanta absorbed by the molecule during its transformation. In this model the activation barrier is two quantum harmonic oscillators having an intersection point, i.e. the top of the barrier [30]. Eq. (5) was used as a transcendental equation for calculating ρ [31]. Combining the two models and the law of conservation of energy made it possible to explain the process of IR multiphoton absorption for the above cases.
With a living cell, the situation is more complicated. All chemical reactions take place in non-equilibrium against the background of thermal equilibrium radiation, light, and radiation energy of metabolic processes occurring in the cell.
Lactate dehydrogenase (LDH) is an enzyme found in nearly all living cells. The LDH catalyzes the reversible reduction of pyruvate to L-lactate using NADH (Nicotinamide Adenine Dinucleotide, Reduced form) as a coenzyme:
Where β-NADH is β-Nicotinamide Adenine Dinucleotide, reduced form; and β-NAD+ is β-Nicotinamide Adenine Dinucleotide, oxidized form.
Increasing the reaction rate by means of additional electromagnetic radiation
Radiofrequency/microwave (RF/MW) radiation: LDH enzyme solutions were irradiated with the MW at three selected frequencies of 1.8, 2.1, 2.3 GHz, power of 10 dBm (power was the same for each studied frequency), and the same room temperature (25 °C) [32]. The results are shown in Table 1.
It should be mentioned that the radiation absorption at the selected frequencies was clearly resonant. That was not the case for another protein example studied in [32], namely Glutathione peroxidase. From this fact, we might reason that the reaction under consideration takes place in three ways, that is, three reactions occur simultaneously.
Let us denote the rate constant of a non-irradiated reaction as Knon rad. It is possible to evaluate the contribution of each of the three reactions to Knon rad. Three differences can be taken:
K1.8 – Knon rad = 5.2392618·1013 Hz– 4.3560146·1013 Hz = 8.832472·1012 Hz,
K2.1 – Knon rad = 6.5842064·1013 Hz – 4.3560146·1013 Hz = 2.2281918·1013 Hz,
K2.3 – Knon rad = 6.2931363·1013 Hz – 4.3560146·1013 Hz = 1.9371217·1013 Hz.
Their sum can now be found:
K1.8 + K2.1 + K2.3 -3·Knon rad = 8.832472·1012 Hz + 2.2281918·1013 Hz +1.9371217·1013 Hz = 5.0485607·1013 Hz.
Knon rad is subtracted from the above result:
5.0485607·1013 Hz – 4.3560146·1013 Hz = 6.925461·1012 Hz.
Supposing our reaction actually consists of three independent one, this value can be divided by 3:
6.925461·1012 Hz /3 = 2.308487·1012 Hz.
Now the rate constants of these reactions can be calculated:
K1.8 – Knon rad - 2.308487·1012 Hz = 8.832472·1012 Hz –2.308487·1012 Hz = 6.523985·1012 Hz,
K2.1 – Knon rad -2.308487·1012 Hz = 2.2281918·1013 Hz – 2.308487·1012 Hz = 1.9973431·1013 Hz,
K2.3 – Knon rad -2.308487·1012 Hz = 1.9371217·1013 Hz – 2.308487·1012 Hz = 1.706273·1013 Hz.
It is easy to check their sum is equal to Knon rad:
6.523985·1012 Hz + 1.9973431·1013 Hz+ 1.706273·1013 Hz= 4.3560146·1013 Hz.
Infrared, visible, ultraviolet light: As in [32], LDH from rabbit muscle, EC1.1.1.27 (Worthington Assay), was selected for experiments. It was found that the LDH activity is selectively increased only by the radiation at the particular wavelengths of 1191 nm, 846 nm [33], 595 nm and 828 nm [34]. The wavelengths of 846 nm and 829 nm are very close. Apparently, their slight difference is due to the conditions of the experiments. The ratio of the solutions components used in [33] and [34] differed somewhat. So it is reasonable to say there are three resonant frequencies for LDH here as well. They determine the values of three activation barriers ΔEa = mhν, while the resonant microwave frequencies 1.8, 2.1, 2.3 GHz are the Einstein spontaneous emission coefficients equal to ν. It is now possible to calculate the number of quantum subsystems m forming a barrier for all the three independent reactions (Table 2). The existence of such subsystems was proved experimentally [35].
The radiation of interest by its nature is associated with dipoles.
Their dipole moments can be derived using the known formula [28,36]:
Arrhenius plots for the specified reactions: Having calculated the values of the reaction rates and their resonant optical frequencies, we can evaluate pre-exponential factors for all the Arrhenius equations:
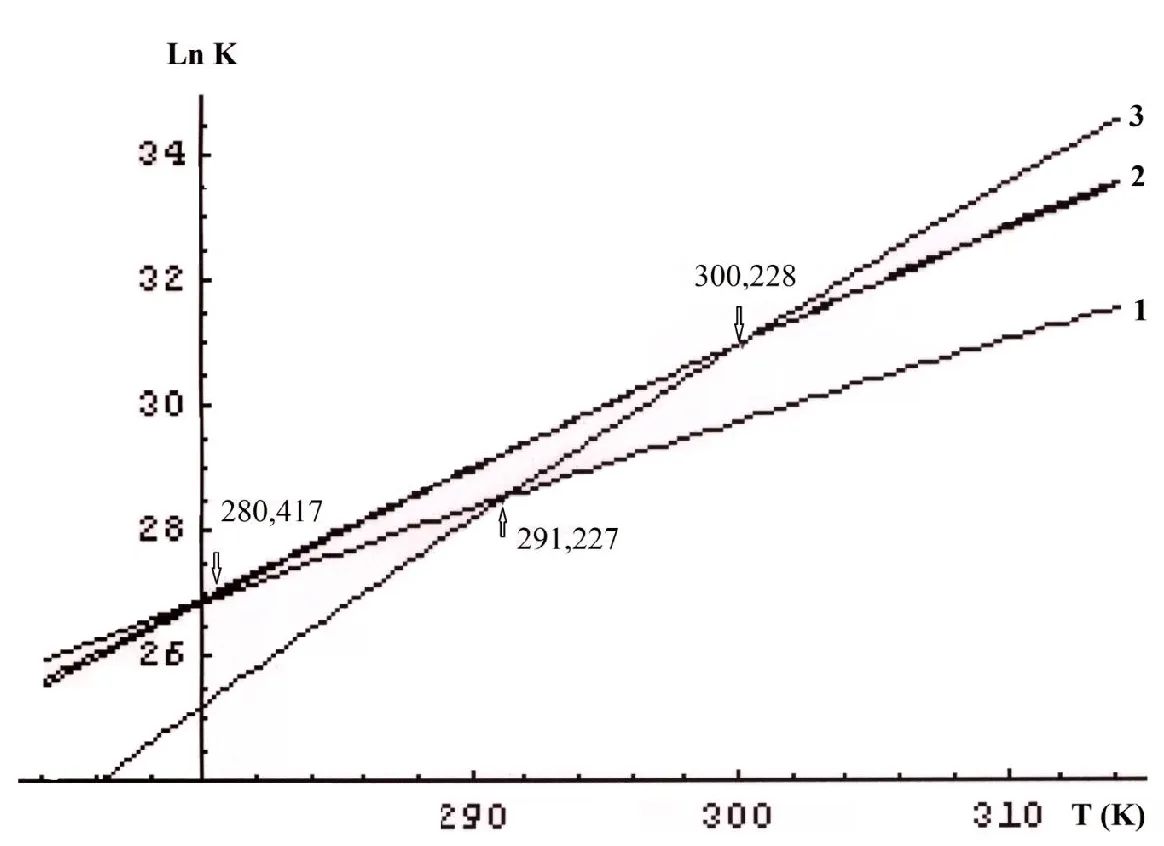
The experimental temperature lies in the range 274.15 to 314.15 K [37,38]. Figure 3 displays plots of ln K versus T. As expected, the reactions with K2.11 и K2.12 rates are actually the same. All the plots have common points of intersection, that is, equal reaction rates at certain temperatures. These temperatures are commonly referred to as compensation temperatures Tcomp. They are indicative of a compensation effect. It was shown that the effect can be associated with a change of degeneracy degrees of vibration levels [26] Table 3.
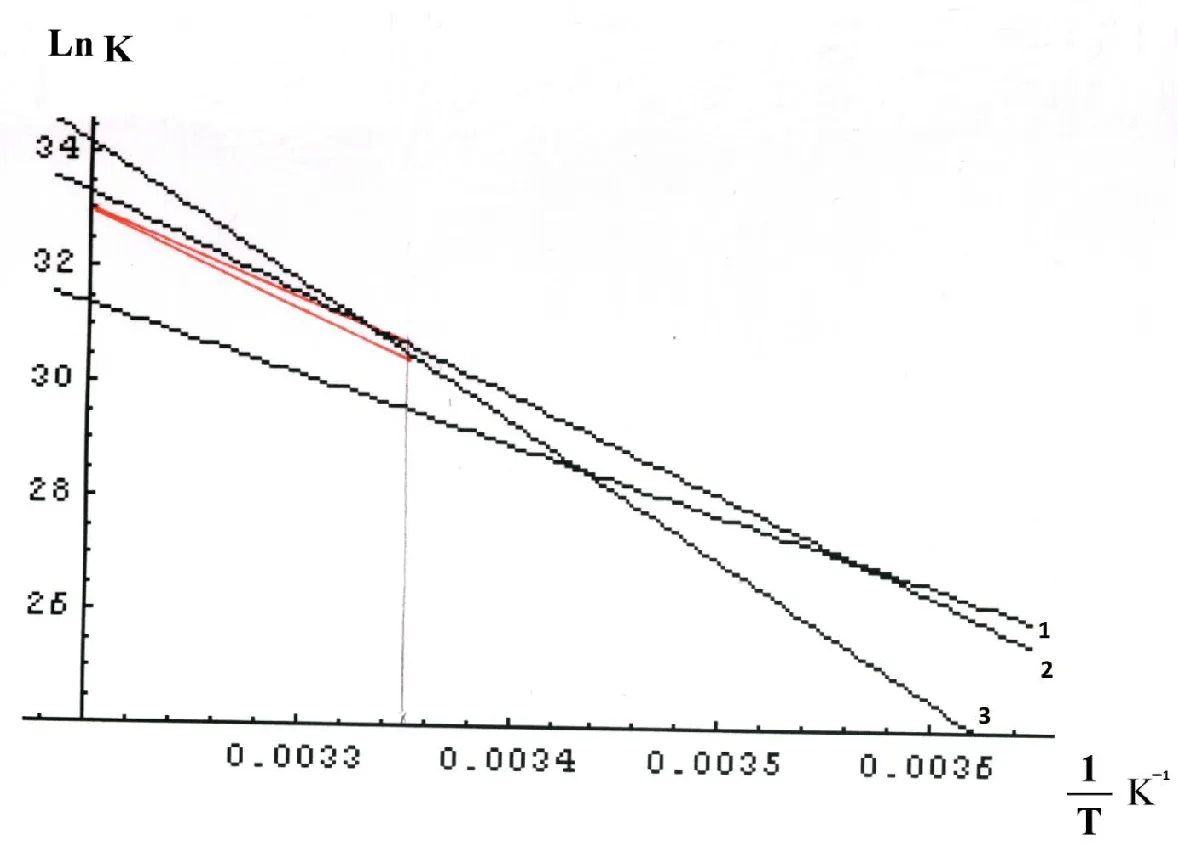
Arrhenius plots for the specified reactions are shown on Figure 4. The plots for 2.1 and 2.3 GHz cases are curved downwards [38]. This peculiarity is pursued further in Section 4.
Distinguishing features of the activation process model for non-equilibrium cases
The model explains the process of energy accumulation necessary for carrying out catalytic reactions in a living cell by means of interaction of quantum subsystems with thermal equilibrium radiation, light, and radiation energy of metabolic processes occurring in the cell.
There are two temperature independent model parameters. These are the quantum subsystem lifetime 1/ν and the activation energy ΔEa = mhν. To account for non-equilibrium, one has to suggest that quantum numbers ξ, η, ζ of the vibration levels as well as their degrees of degeneracy Ω1, Ω2, Ω3 are temperature dependent. As this takes place, pre-exponential factors in Eqs. (6-8) must remain constant. Their values can be calculated using the following formula [26]:
Where A = Ω1m-1, B = Ω2m- Ω1m, C = Ω3m – Ω2m, D = 1-Q-1 , Q=e-mhν/kT at T= 274.15 К, 298.15 К, and 314.15 К. The results are shown in Table 4.
There are two parameters that depend crucially on temperature. These are quantum number ζ for high-energy vibration levels and their degeneracy Ω3. They increase sharply as temperature rises. The same situation happened for dissociation of C8H8+ ions surrounded by intensive infrared laser radiation with the number of laser quanta ρ absorbed by an ion during its transformation [31].
Notice that it is not possible to select the values of ζ and Ω3 for the reactions with K2.1 и K2.3 rates at Т = 314.15 К. Column 4 of Table 4 shows two underlined values of the calculated K0 calc pre-exponential factors that are less than experimental ones (2.317·1038 Hz < 3.813·1038 Hz for ν=2.1·109 Hz, and 5.484·1047 Hz < 2.487·1048 Hz for ν=2.3·109 Hz). If one tries to increase the values of ζ and Ω3, the ones of K0 calc decrease drastically to 2.1·109 Hz and 2.3·109 Hz accordingly. So, there is a threshold as the rate constant increases with temperature. The experimental plots for 2.1 and 2.3 GHz cases are curved downwards at high temperatures [38]. Their theoretical analogues are shown in Figure 4 as red line segments.
As can be seen from column 7 of Table 4, the value of ζ is not necessarily an integer. The same stands for ξ, η, Ω1, Ω2, Ω3, since they are statistical.
Information entropy was calculated using Eq. (4) for all the Arrhenius equations (6-8). The values of Planck and Boltzmann constants were taken to be h = 6,626176·10-34 J·s and k=1.380662·10-23 J/K. The entropy values are divided into two parts. The first part is the information entropy Si of the elementary activation act. It is always positive. The second part Si fuz is negative. It accounts for a measure of energy uncertainty per quantum subsystem, since ζ and Ω3 are temperature dependent. Si fuz can be nullified by selecting the values of Ω3 less than those in Table 4. There is another threshold here similar to that in Fröhlich theory.
Comparing the last two columns of Table 4 one can see the absolute values of Si and Si fuz are the same. This fact ensures the principle of stable non-equilibrium [1] and indicates the reaction under consideration belongs to a living cell [2]. Assume Si is of the order of 10-17-10-18 J/K for every chemical reaction in a living cell at Т ≈ 309.75 К. Then the cell’s information entropy production can be roughly estimated to be 10-9 ÷ 10-8 J/K per second [3].
Conclusion
The results of this report can be summarized as follows:
- L-lactate dehydrogenase kinetics is studied using the activation process model for non-equilibrium cases.
- Lactate dehydrogenase catalyzes the interconversion of pyruvate and lactate with concomitant interconversion of NADH and NAD+ in three ways, that is, three reactions occur simultaneously.
- Each of these reactions has its own values of activation energy and pre-exponential factor for the Arrhenius equation.
- To account for non-equilibrium, one has to suggest that quantum numbers of the vibration levels as well as their degrees of degeneracy are temperature dependent.
- Negative information entropy for the reactions under consideration is calculated. Its absolute value is equal to that of information entropy of the elementary activation act. This fact ensures the principle of stable non-equilibrium and indicates the reaction under consideration belongs to a living cell.
- Bauer ES. Theoretical Biology. Ed. All-Union Institute of Experimental Medicine (VIEM), Moscow. Leningrad. 1935; 151:32.
- Schrodinger E. What is life?The Physical Aspect of the Living Cell. Dublin Institute for Advanced Studies at Trinity College, Dublin. 1943; 33:27.
- https://habr.com/ru/post/424275/. Energy in the cell. Use and storage.
- Himeoka Y, KonekoK. Entropy production of a steady- growth cell with catalytic reactions, arXiv: 1403.3776v1 [q-bio.Sc]. 15 Mar 2014; 1-17.
- Fröhlich H. Bose condensation of strongly excited longitudinal electric modes, Phys. Lett. 1968; 26A: 9; 402:403.
- Fröhlich H. Long-Range Coherence and Energy Storage in Biological Systems., Int. J. Quantum Chem. 1968; II:641-649.
- Fröhlich H. Long range coherence and the action of enzymes. Nature. 1970 Dec 12;228(5276):1093. doi: 10.1038/2281093a0. PMID: 5483165.
- Fröhlich H. Selective long range dispersion forces between large systems, Phys. Lett. 1972; 39A:2; 153:154.
- Fröhlich H. Evidence for Bose condensation – like excitation of coherent modes in biological systems, Phys. Lett. 1975; 51A:1; 21,22.
- Fröhlich H. The extraordinary dielectric properties of biological materials and the action of enzymes. Proc Natl Acad Sci U S A. 1975 Nov;72(11):4211-5. doi: 10.1073/pnas.72.11.4211. PMID: 1060101; PMCID: PMC388689.
- Brown KG, Erfurth SC, Small EW, Peticolas WL. Conformationally dependent low-frequency motions of proteins by laser Raman spectroscopy. Proc Natl Acad Sci U S A. 1972 Jun;69(6):1467-9. doi: 10.1073/pnas.69.6.1467. PMID: 4504361; PMCID: PMC426727.
- Fröhlich H. Long-Range Coherence in Biological Systems, Rivista del Nuovo Cimento. 1977;7:3; 399-418.
- Reimers JR, McKemmish LK, McKenzie RH, Mark AE, Hush NS. Weak, strong, and coherent regimes of Fröhlich condensation and their applications to terahertz medicine and quantum consciousness. Proc Natl Acad Sci U S A. 2009 Mar 17;106(11):4219-24. doi: 10.1073/pnas.0806273106. Epub 2009 Feb 26. PMID: 19251667; PMCID: PMC2657444.
- VasconcellosAR, Vannucchi FS,Mascarenhas S,Luzzi R. Fröhlich Condensate: Emergence of Synergetic Dissipative Structures in Information Processing Biological and Condensed Matter Systems, Information. 2012;.3:601; 620.
- Lundholm IV, Rodilla H, Wahlgren WY, Duelli A, Bourenkov G, Vukusic J, Friedman R, Stake J, Schneider T, Katona G. Terahertz radiation induces non-thermal structural changes associated with Fröhlich condensation in a protein crystal. Struct Dyn. 2015 Oct 13;2(5):054702. doi: 10.1063/1.4931825. PMID: 26798828; PMCID: PMC4711649.
- Nardecchia I,Torres J,Lechelon M,Giliberti V,Ortolani M,Nouvel P,Gori M,Meriquet Y,Donato I,Preto J,Varani L,Sturgis J,Pettini M. Out-of-Equilibrium Collective Oscillation as Phonon Condensation in a Model Protein, Physical Review X. 2018; 8:031061-1:031061-23.
- Zhang Z, AgarwalGS, Scully MO. Quantum fluctuations in Fröhlich condensate of molecular vibrations driven far from equilibrium. arXiv: 1810.07883v1 [quant - ph]. 18 Oct 2018; 1-5.
- Zheng X,Li B. Fröhlich condensate of phonons in optomechanical systems. arXiv: 2101.07723v3 [quant - ph]. 23 Feb 2021; 1-6.
- Fröhlich H. The connection between macro- and micro physics. Rivista del Nuovo Cimento. 1973; 3:490-534.
- GeesinkH JH, Meijer DKF. Quantum wave information of life revealed: an algorithm for electromagnetic frequencies that create stability of biological order, with implications for brain function and Consciousness, NeuroQuantology. 2016; 14:1; 106-125.
- Allec SI, Sun Y, Sun J, Chang CA, Wong BM. Heterogeneous CPU+GPU-Enabled Simulations for DFTB Molecular Dynamics of Large Chemical and Biological Systems. J Chem Theory Comput. 2019 May 14;15(5):2807-2815. doi: 10.1021/acs.jctc.8b01239. Epub 2019 Mar 27. PMID: 30916958; PMCID: PMC8285072.
- Vuong VQ, Cevallos C, Hourahine B, Aradi B, Jakowski J, Irle S, Camacho C. Accelerating the density-functional tight-binding method using graphical processing units. J Chem Phys. 2023 Feb 28;158(8):084802. doi: 10.1063/5.0130797. PMID: 36859078.
- Kumar A, Arantes PR, Saha A, Palermo G, Wong BM. GPU-Enhanced DFTB Metadynamics for Efficiently Predicting Free Energies of Biochemical Systems. Molecules. 2023 Jan 28;28(3):1277. doi: 10.3390/molecules28031277. PMID: 36770943; PMCID: PMC9920250.
- Tavgin VL, Stepanov AV. Activation Process Model, Phys. Stat. Sol. (b). 1990; 161:123-130.
- Tavgin VL, Stepanov AV. Activation process model: application for diffusivity in covalent crystals, Journal of Molecular Structure (Theochem). 1992; 257:1-24.
- Stepanov AV, Tavgin VL. Development of the Activation Process Model: Compensation Effect, International Journal of Quantum Chemistry. 1996; 59:7-14.
- Stepanov AV, Tavgin VL. Simulation of double proton transfer dynamics in benzoic acid dimmer, Journal of Applied Spectroscopy. 2004; 71:4; 462-468.
- Stepanov AV. Activation process model: Einstein coefficients for activation barrier, Journal of Molecular Structure (Theochem). 2007; 85:87-90.
- Stepanov AV, Stepanov MA. Information Entropy of Molecular Tunneling, Conference Proceedings Paper, 4th International Electronic Conference on Entropy and its Applications, 21-November -1st Dectmber 2017; 4:1-12.
- Stepanov AV. What can the activation process model give the adiabatic and non-adiabatic approximation? Journal of Molecular Structure (Theochem). 2001; 538:179-188.
- Stepanov AV. Application of the activation process model to the molecules, positive molecular ions, clusters and proteins surrounded of IR laser radiation, Proc. of SPIE. 2007; 6727:67272 R1 – 67272 R7.
- Alsuhaim HS,Vojisavljevic V,Pirogova E. Effects of low power microwaves at 1.8, 2.1 and 2.3 GHz in l-Lactic dehydrogenase and Glutathione peroxidase enzymes, Journal of Electromagnetic Waves and Applications. 2014; 28:14; 1726-1735.
- Vojisavljevic V, Pirogova E, Cosic I. Influence of electromagnetic radiation on enzyme kinetics. Annu Int Conf IEEE Eng Med Biol Soc. 2007;2007:5021-4. doi: 10.1109/IEMBS.2007.4353468. PMID: 18003134.
- Vojisavljevic V, Pirogova E, Cosic I. The effect of electromagnetic radiation (550-850 nm) on 1-lactate dehydrogenase kinetics. Int J Radiat Biol. 2007 Apr;83(4):221-30. doi: 10.1080/09553000701227565. PMID: 17575949.
- Qiu L, Gulotta M, Callender R. Lactate dehydrogenase undergoes a substantial structural change to bind its substrate. Biophys J. 2007 Sep 1;93(5):1677-86. doi: 10.1529/biophysj.107.109397. Epub 2007 May 4. PMID: 17483169; PMCID: PMC1948838.
- Heitler W. The quantum theory of radiation (Russian edition), IL. 1956; 210.
- Fields PA, Houseman DE. Decreases in activation energy and substrate affinity in cold-adapted A4-lactate dehydrogenase: evidence from the Antarctic notothenioid fish Chaenocephalus aceratus. Mol Biol Evol. 2004 Dec;21(12):2246-55. doi: 10.1093/molbev/msh237. Epub 2004 Aug 18. PMID: 15317880.
- Szasz G. The effect of temperature on enzyme activity and on the affinity of enzymes to their substrates. Z Klin Chem Klin Biochem. 1974 Apr;12(4):166-70. doi: 10.1515/cclm.1974.12.4.166. PMID: 4154546.

Article Alerts
Subscribe to our articles alerts and stay tuned.
 This work is licensed under a Creative Commons Attribution 4.0 International License.
This work is licensed under a Creative Commons Attribution 4.0 International License.

 Save to Mendeley
Save to Mendeley
