International Journal of Nanomaterials, Nanotechnology and Nanomedicine
Simulation of the Behavior of Carbon Nanotori during Unfolding: A Study of Stability and Electronic Structure
Olga E Glukhova* and Michael M Slepchenkov
Cite this as
Glukhova OE, Slepchenkov MM (2018) Simulation of the Behavior of Carbon Nanotori during Unfolding: A Study of Stability and Electronic Structure. Int J Nanomater Nanotechnol Nanomed 4(1): 004-008. DOI: 10.17352/2455-3492.000024In this work, we present an in silico study of the dynamic behavior of a carbon nanotorus during the localized breaking of the C-C bonds in its atomic network. It is shown that the unfolding of a carbon nanotorus is accompanied by the appearance of deformation waves running along the atomic network of the carbon structure. We estimate energy stability of a carbon nanotorus under deformations using the original method for calculating the local stresses of an atomic network. A new physical phenomenon of the molecular current flow in the most deformed sites of the torus atomic network is discovered.
Abbrevations
COMPASS: Condensed-phase Optimized Molecular Potentials for Atomistic Simulation Studies; DOS: Density Of State; SCC DFTB: Self-Consistent Charge Density Functional Tight-Binding; HOMO: Highest Occupied Molecular Orbital
Introduction
Due to geometry and topology features of the atomic structure, the carbon nanotori are considered as prospect objects for many investigations. At present, carbon nanostructures of the given type can be synthesized by the method of laser growth, ultrasound treatment, organic reactions, gas-phase chemical vapor deposition [1-4]. Along with the development of synthesis technologies there are many papers devoted to construct the structural models of toroidal carbon nanostructures. Currently, there are two large classes of the nanotorus structural models. The first class is formed by pristine nanotubes with ideal hexagonal network [5]. The second class is formed by the nanotubes with certain amount of pentagon and heptagon defects [6]. Circular geometry of the structure and incorporation of the defects cause unusual electron [7-9], mechanical and magnetic properties of nanotori as compared to carbon nanotubes.
Due to geometry and topology features of the atomic structure, the carbon nanotori are considered as prospect objects for many investigations. At present, carbon nanostructures of the given type can be synthesized by the method of laser growth, ultrasound treatment, organic reactions, gas-phase chemical vapor deposition [1-4]. Along with the development of synthesis technologies there are many papers devoted to construct the structural models of toroidal carbon nanostructures. Currently, there are two large classes of the nanotorus structural models. The first class is formed by pristine nanotubes with ideal hexagonal network [5]. The second class is formed by the nanotubes with certain amount of pentagon and heptagon defects [6]. Circular geometry of the structure and incorporation of the defects cause unusual electron [7-9], mechanical and magnetic properties of nanotori as compared to carbon nanotubes.
Prediction of stability is very important for the investigation of mechanical properties of toroidal structures, in particular, its behavior under mechanical load. There are a large number of papers devoted to prediction of the nanotori strength features under different deformations [13-15]. For example, C. Feng and K. M. Liew [14], studied behavior of zigzag (9,0) and armchair (8,8) nanotori under mechanical stretching from both sides using COMPASS force field. The critical displacements for the toroidal structure subjected to stretching on two symmetrical sides of the ring were obtained. For armchair tori these values vary from 8.16 nm to 7.9 nm depending on the structure diameter, for zigzag tori – from 0.68 to 2.5 nm. It was found that during stretching the zigzag and armchair tori took the form of an elongated ellipsoid. Influence of structural defects on the strength properties of nanotori was investigated in paper [13]. The behavior of armchair nanotorus (5, 5) with vacancy defect under stretching was modeled within classical molecular dynamics method. Results of numerical experiments have shown that the nanotorus is destroyed with a ratio of displacement to torus diameter larger than 50% independent of the defect concentration. Besides, the loss of stability for toroidal structure and fracture initiation were observed in the area of elongated areas, not in the defect areas. So, all above-mentioned papers did not offer an effective tool for prediction of destruction area in atomic network. At the same time, the influence of deformation on the electronic properties of toroidal structures is still a relevant problem. As shown earlier, it is possible to tune the electronic properties of such carbon structures as graphene nanoribbons [16], and carbon nanotubes [17], using deformation.
The current paper is devoted to solving above mentioned scientific problems. Its main purpose is to study the dynamic deformation processes occurring in carbon nanotorus during local destruction of chemical bonds and to predict the influence of these processes on the electronic properties of carbon nanotori.
Materials and Methods
In order to study the nanotori behavior under deformation we used classical molecular dynamics method with application of modified Brenner potential in order to describe interaction between atoms. As we noted earlier, modified Brenner potential was successfully applied to study deformation processes of graphene nanoobjects under compression and stretching [18]. Nose-Hoover thermostat was applied to control the temperature of medium. All numerical experiments were performed using Kvazar software [19], under 300 K with modeling time-step of 1 fs. In order to study the changes in electronic properties of carbon nanotori during unfolding we calculated density of state (DOS) by means of self-consistent charge density functional tight-binding (SCC DFTB) quantum method [20], using the freely available DFTB+ code [21]. Using the Mulliken population analysis [22] we estimated valence electron charge density of carbon atoms during nanotorus unfolding.
Results and Discussion
Molecular-dynamic simulation of the nanotorus unfolding
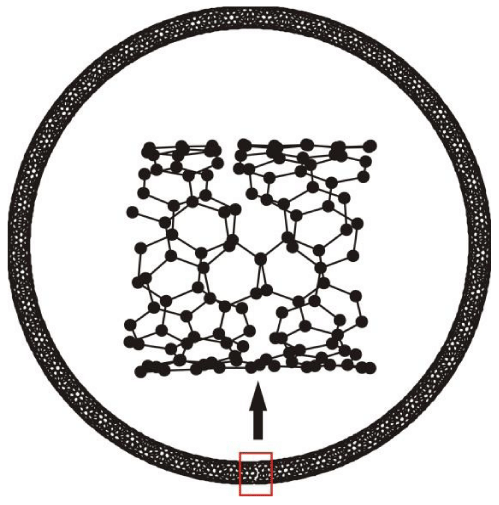
The object of this study was carbon nanotorus (10, 6) with the diameter of 20 nm and thickness of 1 nm. This torus was obtained as a result of defectless folding of chiral nanotube with corresponding geometry sizes into ring. Such structures can be synthesized by a high-voltage pulsed discharge in ethanol vapor [23]. In our numerical experiment, the chemical bonds were destroyed on the circle of the tube in a fixed fragment of the torus atomic network as shown in figure 1. Such localized destructions can occur during the synthesis of tori when the chemical bonds of the structure are destroyed under external factors (pressure, temperature, arc discharge and others), and torus is, in fact, broken. Also, these destructions may be caused by an action of atomic force microscope tip during probing the surface of synthesized carbon object. We were interested in two questions in the course of the study of torus dynamic behavior: how the atomic structure of the torus would be reconstructed over time of the numerical experiment and how this will change the energy stability of the investigated structure.
Figure 2 shows investigated nanotorus after bond breakage in fixed times. It can be seen from the figure that during the first 30 ps three sections of different form were clearly distinguished in the object structure: central part in the form of arc, and two edge parts with the form close to straight. Transition zones between sections form bends that spread from the object edges to its center like waves with velocity of 200 m/s. After ~30 ps the deformation waves reached the structure center and form the bend of complex form with two almost straight sites on its edge. After ~60 ps the central part of the object was straightened, and then structure gradually took the form of deformed tube. After the bonds were destroyed, the torus straightened into the tube within 91 ps.
In order to estimate the influence of deformation waves spreading in atomic framework on the toroidal objects stability we calculated field of local stresses. These calculations were performed by means of original method, which applied earlier to study the stability of graphene nanoribbons under axial compression [16] and bamboo-like nanotubes [17]. By stress at atom we mean the difference between energy density of a torus and energy density of a nanotube, which form the torus. The following algorithm was used to calculate a local stress:
1) Optimization of initial atomic structure of a carbon nanotube by minimization of the total energy using empirical method based on the Brenner potential;
2) Calculation of distribution of the bulk energy density on nanotube’s atoms;
3) Optimization of the structure of a nanotorus formatted in the result of the nanotube unfolding by minimization of the total energy;
4) Calculation of the bulk energy density distribution on nanotorus’ atoms;
5) Calculation of the local stress field by difference of the bulk energy density for a torus and a nanotube. The local stress for atom with number i was calculated according to formula:
where is the bulk energy density of a nanotube which form the torus, is the bulk energy density of a torus.
Figure 3 shows fragments of atomic framework in different time moments with different degrees of deformation. The stress distribution on torus’ atoms is shown by color for different fragments. The sharp bends of the atomic network are observed during the spread of deformation wave. They appear for several picoseconds. In these local areas of the atomic framework the stress increases up to 18 GPa on some atoms. This value exceeds critical value for the nanotubes (14 GPa [17]), that’s why some chemical bonds are broken. Such areas of atomic framework are highlighted by red at the picture. Since the deformation wave moves with large velocity, the structure can’t relax to minimum energy and the bonds are restored in the next time. We suggest that this interest physical phenomenon is observed within whole process of torus unfolding. During torus unfolding the value of maximum stress decreases and reaches minimum in the moment of final torus straightening.
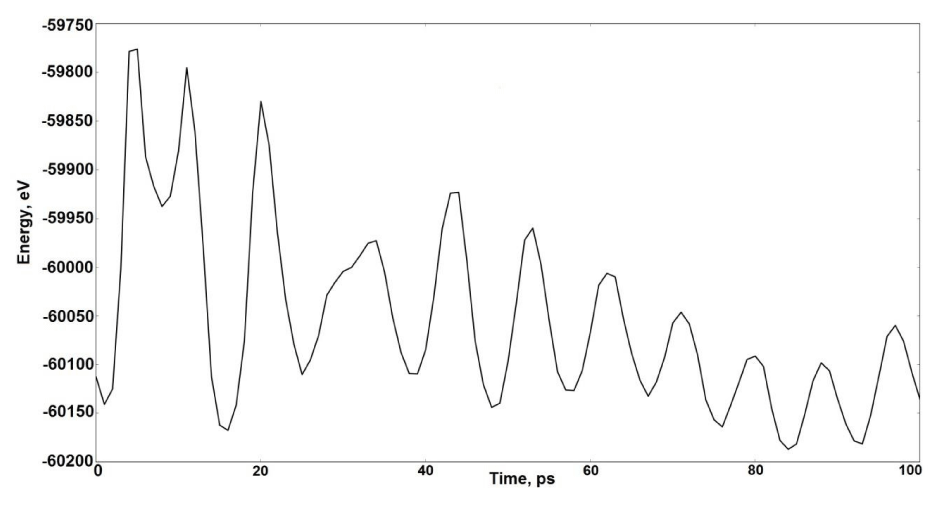
The stress peaks occurred in atomic network affect the energy. Figure 4 shows plot of energy change during unfolding a chiral torus into tube. This plot shows that the sharp jump of energy is observed in the moment of torus breaking. This jump is caused by a repulsion of opened torus edges. Further, the total energy of the structure decreases uniformly right up until the final nanotorus straightening.
Prediction of changes in the electronic properties of a chiral nanotorus during unfolding
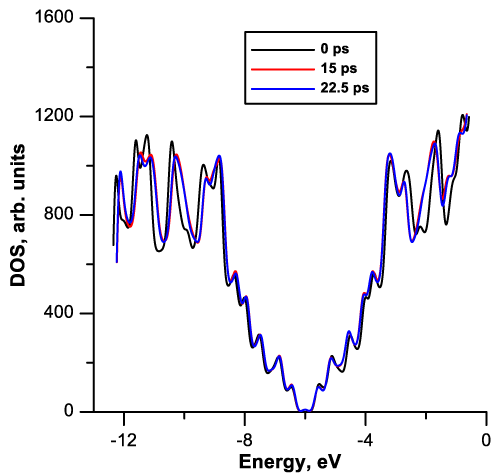
In order to identify the effect of the deformation wave on the electronic properties of a carbon torus, we calculated DOS. Figure 5 shows the DOS of the nanotorus at fixed time moments. In these moments, we observed the sharpest bends of the atomic network of toroidal structures. The time of 10 ps correspondWs to the case when two symmetrical sharp bends were formed in the atomic network of a torus. The time of 22.5 ps corresponds to the case when one bend of complex shape was formed in the atomic network of a torus. As can be seen from the graph, there are no visible changes in the DOS distribution for the deformed nanotorus at the transition from two sharp bends of the framework to one bend of the complex shape formed in the region of the closing deformation waves moving towards each other.
The DOS distributions were calculated for the original defectless chiral torus and the corresponding chiral tube in order to estimate the changes in the electronic properties of a torus during the propagation of deformation waves along its framework. The calculation results are shown in figure 6a. As can be seen from this figure, the DOS distributions for the nanotube and torus have a pronounced similarity. However, in the electronic structure of the torus there is an important change in comparison with the nanotube structure, namely, the appearance of an energy gap of 0.5 eV. Figure 6b shows an isolated fragment of the DOS distribution near the Highest Occupied Molecular Orbital (HOMO) level, clearly illustrating the appearance of an energy gap in the electronic structure of a defectless chiral nanotorus. Also, this figure shows a fragment of the DOS distribution of a straightening nanotorus at the time of the largest bending of the atomic network. Analyzing the presented results of the DOS distributions, we can conclude that as soon as the torus loses the integrity of its atomic framework and ceases to be a closed structure, it loses semiconductor properties and becomes a conductor.
Further, we estimated valence electron charge density of carbon atoms during nanotorus straightening using the Mulliken population analysis [23]. In the course of the study, it was found that the charge transfer between the carbon atoms of the deformed framework was observed with the nanotorus straightening. The maximum values of the electron charge transfer (~ 0.05e ~ 0.09e) were found in the regions of the largest bends of the atomic structure of the torus. The maximum stresses are also concentrated in these structural regions. This fact is due to the previously established relationship between the mechanical characteristic and the electron density of the atomic framework [16]. According to our previous results obtained for carbon nanostructures, the rehybridization electronic orbitals will be stronger in the areas of the largest curvature of the surface. That is why the largest charge transfer is fixed in the region of the largest curvature of the atomic grid of the torus as a consequence of deformation. Using the maximum value of the electron charge flow, we numerically determined the amount of current flowing in the carbon nanotorus during its straightening. Figure 7 shows the dynamics of the current change during relaxation time of the toroidal structure.
It can be seen from the above plot, the maximum value of the current (~ 1.1 nA) is reached 7.5 ps after localized breaking the chemical bonds on a circle of the nanotorus. At this time, the atomic structure of the torus is characterized by the presence of four symmetrical bends of the framework. As the torus is straightened, the current begins to decrease, reaching a minimum at the instant of the disappearance of the sharp bends of the atomic network.
Conclusion
The phenomenon of formation and propagation of deformation waves in the toroidal nanostructures was revealed during the study of dynamic behavior of a chiral nanotorus at localized destruction of the chemical bonds of the atomic network. These waves appear after breaking torus and lead to its deformations and numerous local bond breaks. Since the deformation wave moves along the atomic framework of the torus with a high velocity (~ 200 m/s), the toroidal structure does not have time to relax to a minimum of energy, and the chemical bonds are restored at the next time. In this regard, the atomic framework of the torus remains defect-free after being unfolded into the tube. The results of calculation of the local stress distribution indicate that the straightened torus is characterized by high energy stability. The time of the full unfolding process for a chiral torus with a diameter of 20 nm is ~ 91 ps.
Analysis of the calculation results of the DOS distribution showed that at the instant of localized breaking of chemical bonds along the circumference of the tubular framework, the torus loses its semiconductor properties and become a clearly expressed conductor. During a study of electron charge distribution at different instants of the unfolding of a nanotorus, we found a new physical effect, consisting in that the molecular current flows in the torus atomic network sections that have undergone the greatest deformations. The maximum value of the current depends on the degree of deformation of the atomic framework.
Thus, the obtained results allow us to consider carbon nanotori as a promising material for nanoelectronics that is resistant to mechanical stresses and deformations.
The work was supported by Russian Presidential scholarship 2016-2018 (project No. СП-3135.2016.1).
- Vimalanathan K, Chena X, Raston CL (2014) Shear induced fabrication of intertwined single walled carbon nanotube rings. Chem Commun 50: 11295-11298. Link: https://goo.gl/uDXeg3
- Lee J, Baek K, Kim M, Yun G, Ko YH, et al. (2014) Hollow nanotubular toroidal polymer microrings. Nature Chemistry 6: 97-103. Link: https://goo.gl/yREYzT
- Sonay AY, Culha M (2013) DNA-mediated self-assembly of single-walled carbon nanotubes into nanorings. Small 9: 2059-2063. Link: https://goo.gl/AwRwzJ
- Wang W, Laird ED, Gogotsi Y, Li CY (2012) Bending single-walled carbon nanotubes into nanorings using a Pickering emulsion-based process. Carbon 50: 1769-1775. Link: https://goo.gl/yzS5Ns
- Chuang C, Fan YC, Jin BY (2009) Generalized Classification Scheme of Toroidal and Helical Carbon Nanotubes. J Chem Inf Model 49: 361-368. Link: https://goo.gl/mnJVN3
- Alisafaei F, Ansari R, Alipour A (2014) A semi-analytical approach for the interaction of carbon nanotori. Physica E 58: 63-66. Link: https://goo.gl/vTCWZD
- Liu L, Liu F, Zhao J (2014) Curved carbon nanotubes: From unique geometries to novel properties and peculiar applications. Nano Research 7: 626-657. Link: https://goo.gl/sCE4Vt
- Feng C, Liew KM (2010) Buckling Behavior of Armchair and Zigzag Carbon Nanorings. J Comput Theor Nanosci 7: 2049-2053. Link: https://goo.gl/sehxwQ
- Chen H, Zhang E, Zhanga K, Zhang S (2015) The Aharonov–Bohm effect in the carbon nanotube ring. RSC Advances 5: 45551-45557. Link: https://goo.gl/RYyDX1
- Chuang C, Guan J, Witalka D, Zhu Z, Jin BY, et al. (2015) Relative stability and local curvature analysis in carbon nanotori. Phys Rev B 91: 165433. Link: https://goo.gl/8SXY51
- Liu L, Zhang L, Gao H, Zhao J (2011) Structure, energetics, and heteroatom doping of armchair carbon nanotori. Carbon 49: 4518-4523. Link: https://goo.gl/i6J7RF
- Liu P, Zhang YW A (2010) Theoretical analysis of the effect of a Stone-Thrower-Wales defect on the stability of carbon nanotube-based nanorings. Carbon 48: 2225-2230. Link: https://goo.gl/KF9Ah5
- Feng C, Liew KM (2011) Fracture Properties of Defective Carbon Nanorings. J Comput Theor Nanosci 8: 1–7. Link: https://goo.gl/zyokN3
- Feng C, Liew KM (2010) Buckling Behavior of Armchair and Zigzag Carbon Nanorings. J Comput Theor Nanosci 7: 2049-2053. Link: https://goo.gl/SeNCH8
- Feng C, Liew KM (2009) A molecular mechanics analysis of the buckling behavior of carbon nanorings under tension. Carbon 47: 3508-3514. Link: https://goo.gl/95TpQ6
- Glukhova O, Slepchenkov M (2012) Influence of the curvature of deformed graphene nanoribbons on their electronic and adsorptive properties: theoretical investigation based on the analysis of the local stress field for an atomic grid. Nanoscale 4: 3335-3344. Link: https://goo.gl/rT6kSz
- Glukhova OE, Kolesnikova AS, Slepchenkov MM (2013) Stability of the thin partitioned carbon nanotubes. J Mol Model 19: 4369-4375. Link: https://goo.gl/wymNo6
- Glukhova OE, Kolesnikova AS (2011) Empirical Modelling of Longitudinal Tension and Compression of Graphene Nanoparticles and Nanoribbons. Phys Solid State 53: 1957-1962. Link: https://goo.gl/piJSS7
- Glukhova OE (2017) Molecular Dynamics as the Tool for Investigation of Carbon Nanostructures Properties. Thermal Transport in Carbon-Based Nanomaterials by Editor Gang Zhang. Elsevier 2017: 267-290. Link: https://goo.gl/242JpY
- Elstner M, Seifert G (2014) Density functional tight binding. Phil Trans R Soc A 372: 20120483. Link: https://goo.gl/xgg1Tj
- Density Functional based tight Binding (and more). Link: https://goo.gl/jXgNmk
- Carbó-Dorca R, Bultinck P (2004) Quantum Mechanical Basis for Mulliken Population Analysis. J Mat Chem 36: 231-239. Link: https://goo.gl/qVVy7s
- Glukhova OE, Kondrashov VA, Nevolin VK, Bobrinetsky II, Savostyanov GV, et al. (2016) Prediction of the stability and electronic properties of carbon nanotori synthesized by a high-voltage pulsed discharge in ethanol vapor. Semiconductors 50: 502-507. Link: https://goo.gl/csfWUf

Article Alerts
Subscribe to our articles alerts and stay tuned.
 This work is licensed under a Creative Commons Attribution 4.0 International License.
This work is licensed under a Creative Commons Attribution 4.0 International License.

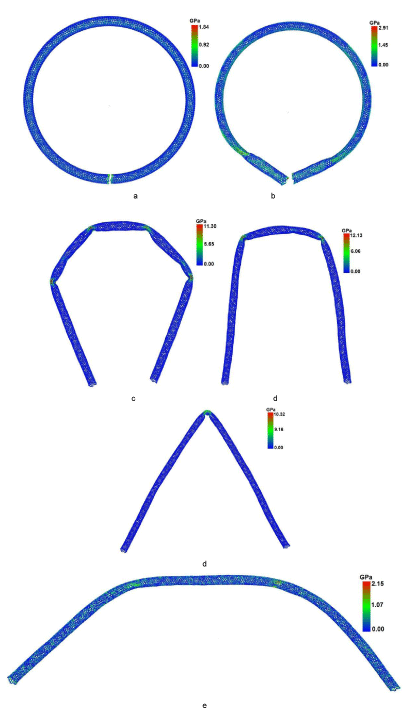
 Save to Mendeley
Save to Mendeley
