Study the effect of different shapes of plume rise on Gaussian plume models and its maximum in unstable conditions

Exposure to radioactive pollutants such as Iodine-135 I¹³⁵ seriously threatens public health and environmental balance. Monitoring and managing these pollutants require expensive economic equipment that is not suitable for low-income countries such as Egypt. Therefore, trying to derive a mathematical model that estimates the concentrations of these radioactive pollutants with high accuracy and a low relative error coefficient compared to the actually measured values ​​is very important. Therefore a mathematical Gaussian model was received to estimate the concentrations of I¹³⁵ emitted from the research nuclear reactor in the Inshas region in Egypt using different shapes of plume rise in unstable conditions.

A comparison between the derived model and its maximum values with observed concentrations data measuring on Egyptian Atomic Energy Authority for I¹³⁵ in unstable conditions has been found. The derived model may be applied to estimate and predict the emissions of any radioactive pollutant for any similar area and similar type of used reactor, which provides high-precision technology with zero economic cost.

The statistical technique shows that the entire Gaussian model and its maximum inside a factor of two with observed concentration data achieved 98%. In addition, the statistics show that all the Gaussian plume models and their maximum have a correlation coefficient of about 0.95%. Also, the normalized mean square error. And the fraction bias. are near-zero values in all Gaussian models and their maximum.

Introduction

A simple model for atmospheric dispersion in short-range (up to 10 km from the source) is the Gaussian plume model as said by Curtiss and Rabl in 1996 [1]. But in 1995, Sharan, et al. [2] established that conventional approaches for estimating plume-dispersion parameters are the least likely to be suitable for operation under low wind speed and stable conditions. Gaussian-plume models play a major part in the nonsupervisory area. Still, they may not always be the smart models to use and it was noted at the 15th International Clean Air Conference 2000 – Modeling Workshop that particular models aren’t always chosen on an objective scientific base Ross [3]. Abdel-Rahman [4] studied the atmospheric dispersion and Gaussian plume model. Essa, et al. [5] studied the plume rise and wind speed effect on the extreme value of air contaminant concentration.

In artificial operations, the classical Gaussian diffusion models are substantially used in effecting the impacts of finding and proposed sources of air pollutants on local and urban air quality by Arya [6]. Homeliness, associated with the Gaussian logical model, does this approach particularly suitable for organizational operation in the fine modeling of air pollution. Indeed, similar models are relatively useful in short-range soothsaying. The side and perpendicular dissipation parameters, independently σ_y and σ_z, represent the crucial turbulent parameterization in this approach, once they contain the physical constituents that describe the dissipation process and, accordingly, express the spatial extent of the adulterant premium under the effect of the turbulent stir in the (‘Planetary boundary layer’) Abdul-Wahab [7].

The atmospheric advection- prolixity equation had long been made to know the transport of adulterants in a turbulent atmosphere was studied by Seinfeld [8]. A logical dissipation Model for sources in the atmospheric face subcaste with a dry deposit to the ground face has been studied by Kumar and Sharan [9]. Also researched the variation of circle diffusivity on the mimics of the geste of advection- prolixity equation was studied by Essa, et al. [10]. Essa, et al. [11] answered the advection- prolixity equation with variable perpendicular circle diffusivity and wind speed using Hankel transfigure to get the crosswind integrated attention.

This work studies the effect of premium rise on Gaussian premium models and their outside using different shapes of dissipation parameters and premium rise. After that, we used the Gaussian premium model, its outside, and compared it with observed attention data which are taken from the Egyptian Atomic Energy Authority for Iodine-135 I¹³⁵ in an unstable condition.

Mathematical models

The Gaussian model concentration can be written [12] as follows:

$C\left(x,y,z\right)=\frac{Q}{2\pi u{\sigma }_y{\sigma }_z}{e}^{\frac{-y^2}{2{\sigma }_y^2}}[e^{\frac{-{(z-H)}^2}{2{\sigma }_z^2}}+e^{\frac{-{\left(z+H\right)}^2}{2{\sigma }_z^2}}]e^{-\frac{\upsilon x}{u}}\text{ (1)}$

Where, $e^{-\upsilon x/u}$ is the radioactive decay for isotope, υ = 2.9 x 10^-5 s^-1 for Iodine-135.

Where σ_y and σ_z are the dispersion parameters in crosswind and vertical directions of the plume respectively, Q is the emission rate, H is the effective stack height; $H=h_s+\Delta h,$ hs is the stack height and ∆h is the plume rise, u is the mean wind speed, while y and z are the crosswinds and the vertical coordinates, respectively.

Maximum Gaussian concentration has the form:

${\text{C}}_{\text{max}}=\frac{\text{Q}}{{\text{πuσ}}_{\text{y}}{\text{σ}}_{\text{z}}}{\text{e}}^{-\frac{{\text{H}}^2}{2{\text{σ}}_{\text{z}}^2}}\text{ (2)}$

Where,

${\sigma }_z=\frac{H}{\sqrt{2}}$

The mean concentration of pollutant plumes emitted from a point source can be assumed to have a Gaussian distribution which is highly idealized since they require stationary and homogeneous turbulence in the PBL ‘Planetary boundary layer’ where the flow may be assumed quasi-stationary for suitable short periods (from 10 min to 1 h) Yves, et al. [13].

Using the different dispersion parameters of σy and σz in each of the two cases:

The first crosswind and vertical dispersion parameters for the convective condition are taken from the previous work of Lidiane, et al. in [14] with the form:

$\frac{{\text{σ}}_{\text{y}}^2}{{\text{h}}^2}=\frac{0.55{\text{X}}^2{\text{Ψ}}^{\frac{2}{3}}}{1+\left(2.2{\text{XΨ}}^{\frac{1}{3}}\right)}\text{ (3)}$

$\frac{{\text{σ}}_{\text{z}}^2}{{\text{h}}^2}=\frac{0.42{\text{X}}^2{\text{Ψ}}^{\frac{2}{3}}}{1+\left(2.9{\text{XΨ}}^{\frac{1}{3}}\right)}\text{ (4)}$

Where; $\text{Ψ}=\frac{\epsilon h}{w_{*}^3}$ ; ε is the mean dissipation rate of turbulence kinetic energy per unit time per unit mass of fluid, Field observations in a convective PBL show that 0.65 by Cauchey and Palmer [15]. $X=\frac{x{w}_{*}}{uh}$ is a non-dimensional distance defined by the travel time to the convective time scale and h is mixing height.

The second crosswind and vertical dispersion parameters for the convective condition are taken from Lidiane, et al. [16] in the form:

$\frac{{\sigma }_y^2}{h^2}=\frac{0.66}{{\pi }^2}\underset{0}{\overset{\infty }{{\displaystyle \int }}}\frac{{\sin }^2\left(0.75\pi {\text{Ψ}}^{\frac{1}{3}}X\acute{n}\right)}{{\acute{n}}^2{\left(1+\acute{n}\right)}^{\frac{5}{3}}}d\acute{n}\text{ (5)}$

$\frac{{\sigma }_z^2}{h^2}=\frac{0.98}{{\pi }^2}\underset{0}{\overset{\infty }{{\displaystyle \int }}}\frac{{\sin }^2\left(0.98\pi {\text{Ψ}}^{\frac{1}{3}}X\acute{n}\right)}{{\acute{n}}^2{\left(1+\acute{n}\right)}^{\frac{5}{3}}}d\acute{n}\text{ (6)}$

Where, $\acute{n}=\frac{1.5z}{u {\left(f_m^{*}\right)}_i}n$ ; ${\left(f_m^{*}\right)}_i$ is the reduced frequency of the convective spectral peak in the form

${\left(f_m^{*}\right)}_i=\frac{z}{h}.$

First:

$H=h{\text{}}_s+\Delta h=h_s+3(w/u)D\text{ (7)}$

Where w is the exit velocity of the pollutants (4 m/s), D is the internal stack diameter, and h_s is the stack height (43 m)

Second:

Briggs plume rise

∆h = 150 F / u ^ 3 (8)

Where,

F = g w (D / 2) ^ 2 (Ts - Ta)

Where; F is the buoyancy flux parameter, Ambient temperature (Ta)- 25 0C-, Stack temperature (T_s) – 50 0C-.

Third:

Carson and Moses equation:

∆h = 3.47 w D/u + 5.15 Qh^0.5/u. (9)

Where,

Q_h = Heat emission rate in 5000 K.cal/sec

Results and statistical technique

Air samples were collected around the Egyptian Atomic Energy Authority. The vertical height is 0.7 m above ground from a stack height of 43 m, for twenty-four hours of working, where the air samples were collected for a half-hour at a height of 0.7m with a roughness length of 0.6 cm. The values of ‘n’ are a function of air stability are taken from Hanna, et al. [16]. The observed data of I¹³⁵ isotope concentration was obtained from dispersion as experiments conducted in unstable conditions (82) and presented in Table 1. The observed concentration of the I¹³⁵ isotope and the meteorological data during the experiments are taken from Essa and El-Otaify [17] and presented in Table 2. The predicted concentrations by Eqns. (1,3,4,7), (1,5,6,7), (1,3,4,8), (1,5,6,8), and (1,3,4,9), (1,5,6,9) below the plume centerline are also presented in Table (3). Also, The predicted maximum concentrations by Eqns. (2,3,4,7), (2,5,6,7), (2,3,4,8), (2,5,6,8) and (2,3,4,9), (2,5,6,9) below the plume centerline are also presented in Tables 3-5.

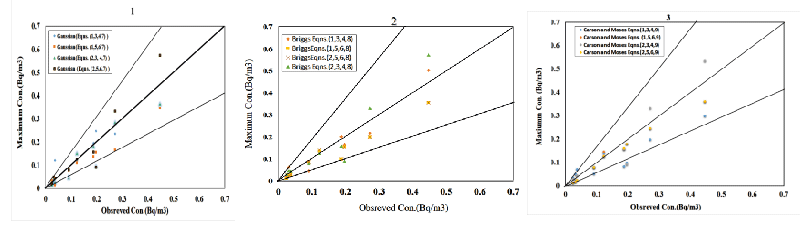
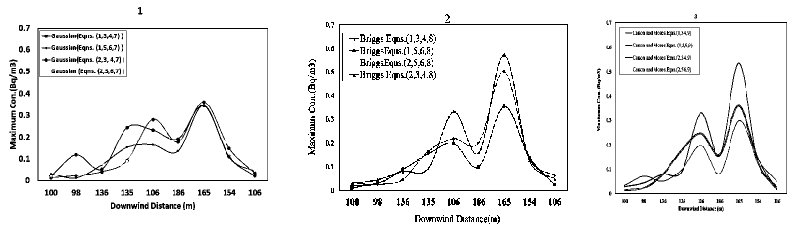
A comparison between predicted and observed concentrations of radioactive I¹³⁵ via downwind distance in unstable conditions at Inshas is shown in Figure 1A, also, the relation between predicted and observed concentration data are shown in Figure 1B. Comparison between observed and predicted, maximum concentrations for different plume rises in an unstable condition. is introduced by [18-20]. Where NMSE is the normalized mean square error, FB is the fraction bias, COR is the correlation coefficient and FAC2 is the factor of two in Table 6, where NMSE is the Normalized Mean Square Error factor of two, the statistical technique shows that the entire Gaussian models and their maximum inside a factor of two with observed concentration data achieved 98%. In addition, the statistics show that all the Gaussian plume models and their maximum have a correlation coefficient of about 0.95%. Also, the normalized mean square error and The Fraction Bias are near-zero values in all Gaussian models and their maximum. Equations (1,3,4,8) of the Gaussian plume model with Briggs plume rise is the best statistical technique than other plume rises. In addition, Equations (2,5,6,9) of the maximum Gaussian plume model with Carson and Moses equation is the best statistical technique than other plume rises.

Figure 1A: 1-3- Comparison between Observed, calculated, maximum concentration for different Gaussian, Briggs and Carson, and Moses in an unstable plume rise.

Figure 1B: 1-3- Comparison between Observed, calculated, maximum concentration, and downwind distance for different Gaussian, Briggs and Carson and Moses in an unstable plume rise.

Discussion

One finds that the Gaussian concentrations agree well with the observed concentrations of I¹³⁵ over downwind distance as shown in Supplementary Figures 1A-3A and its maximum Gaussian concentration. In addition, we find that the Gaussian concentrations and their peak values are within a factor of two with the observed concentrations of I¹³⁵ as shown in the three Figures 1B-3B. Statistics show that all Gaussian column and max models have a correlation coefficient of about 0.95%. Also, normalized mean squared error and fraction bias are values close to zero in all Gaussian models and their maximum. Equations (1,3,4, and 8) of a Gaussian plume model with Briggs plume height is a better statistical technique than other column heights. In addition, equations (2,5,6, and 9) of the maximum Gaussian model with the Carson and Moses equation are a better statistical technique than other plume heights.

Conclusion

This work studies the effectiveness of three plume rises on Gaussian plume models and their maximum. The Gaussian concentrations plume models and their maximum values are lying inside a factor of two with the observed concentrations measured on Egyptian Atomic Energy Authority for Iodine-135 I¹³⁵ in an unstable condition.

The statistical technique shows that the entire Gaussian model and its maximum inside a factor of two with observed concentration data achieved 98%. In addition, the statistics show that all the Gaussian plume models and their maximum have a correlation coefficient of about 0.95%. Also, the Normalized Mean Square Error and The Fraction Bias are near-zero values in all Gaussian models and their maximum.

Availability of data and material

The data that support the findings of this study are available from the Egyptian Environmental Affairs Agency and the Egyptian Meteorological Authority but restrictions apply to the availability of these data, which were used under license for the current study, and so are not publicly available. However, data are available from the authors upon reasonable request and with permission of both the Egyptian Environmental Affairs Agency and the Egyptian Meteorological Authority.

Author’s contributions

K.E. conceived the experiments, S. E. conducted the experiments, and A.W and M.E. analyzed the results. All authors read and approved the final manuscript.

The authors are expressing their gratitude to the Egyptian Knowledge Bank and Academy of Science, Research and Technology for supporting the authors in funding the publishing of this article.

1. Curtiss PS, Rabl A. Impacts of air pollution: general relationships and site dependence. Atmospheric Environment. 1996; 30(19):3331–3347.
2. Sharan M, Yadav AK, Singh MP. Comparison of sigma schemes for estimation of air pollutant dispersion in low winds. Atmospheric Environment. 1995; 29(16):2051–2059.
3. Ross D. Modelling workshop report. Clean Air and Environmental Quality. 2001; 35(3):26–27. https://search.informit.org/doi/10.3316/informit.135004118970669
4. Abdel-Rahman AA. On the Atmospheric Dispersion and Gaussian Plume Model, Waste Management, Water Pollution, Air Pollution, Indoor Climate, 2nd International Conference, Corfu, Greece. October 26-28, 2008.
5. Essa Khaled SM, Mubarak F, Elsaid SEM. Effect of the plume rise and wind speed on extreme value of air pollutant concentration. Meteorol. Atmos. Phys. 2006; 93:247–253. 10.1007/s00703-005-0168-1
6. Arya S. Air Pollution Meteorology and Dispersion. Oxford University Press. 1999; 310.
7. Abdul-Wahab SA. The Role of Meteorology in Predicting SO2 Concentrations around a Refinery: An Oman Case Study, Ecol. Modell. 2006; 197: 13-20.
8. Seinfeld JH. ES Books: Atmospheric Chemistry and Physics of Air Pollution. Environ Sci Technol. 1986 Sep 1;20(9):863. doi: 10.1021/es00151a602. PMID: 22263816.
9. Kumar P, Sharan M. An Analytical Dispersion Model for Sources in the Atmospheric Surface Layer with Dry Deposition to the Ground Surface”. Aerosol and Air Quality Research. 2016; 16:1284–1293.
10. Khaled E, Aziz M, Hany H, Fawzia M, Ayman k. Studying the variation of eddy diffusivity on the behavior of advection-diffusion equation. NRIAG Journal of Astronomy and Geophysics. 2018; 7 (1):10-14. 10.1016/j.nrjag.2018.02.003
11. Essa KSM, Shalaby AS, Ibrahim MAE, Mosallem AM. Analytical solutions of the advection-diffusion equation with variable vertical Eddy diffusivity and wind speed using Hankel transform. Pure and Applied Geophysics. 2020; 17:4545-4557. https://doi.org /10.1007/s00024-020-02496-y.
12. Abd El-Wahab MM, Khaled SM. Essa HM Elsman, Soliman ASh, Elgmmal SM, wheida AA. Derivation of the Gaussian plume model in three dimensions. MAUSAM. 2014; 65:1; 83-92.
13. Jannot Y, Lasseux D. A new quasi-steady method to measure gas permeability of weakly permeable porous media. Rev Sci Instrum. 2012 Jan;83(1):015113. doi: 10.1063/1.3677846. PMID: 22299992.
14. Buligon L, Degrazia GA, Szinvelski CRP, Goulart A. Algebraic Formulation for the Dispersion Parameters in an Unstable Planetary Boundary Layer: Application in the Air Pollution Gaussian model. The Open Atmospheric Science Journal. 2008; 2:153-159.
15. Cauchey SJ, Palmer SG. Some aspects of turbulence structure through the depth of the convective boundary layer. QJR. Meteorol Soc. 1979; 105: 811-27.
16. Hanna SR, Briggs GA, Hosker Jr RP. Handbook on atmospheric diffusion. United States. 1982. 10.2172/5591108
17. Essa Khaled SM, El-Otaify Maha S. Atmospheric vertical dispersion in moderate winds with eddy diffusivities as power-law functions. Meteorologische Zeitschrift. 2008; 17 (1):13–18.
18. Hanna SR. Confidence limits for air quality model evaluations, as estimated by bootstrap and jackknife resampling methods. Atmospheric Environment. 1989; 23(6):1385–1398. 0.1016/0004-6981(89)90161-3
19. Buligon L, Gervásio D, Szinvelskia A, Charles RP, Goulart Antonio G. Algebraic Formulation for the Dispersion Parameters in an Unstable Planetary Boundary Layer: Application in the Air Pollution Gaussian Model. The Open Atmospheric Science Journal. 2008; 2:153-159.
20. Khaled E, Ahmed M, Ahmed S. Evaluation of analytical solution of advection diffusion equation in three dimensions. Atmospheric Science Letters. 2021; 22 (1). 10.1002/asl.1043