On population-space description of chemical reactivity

The electron-population degrees-of-freedom of donor-acceptor systems are reexamined and alternative simple models of charge-transfer reactivity are discussed in the substrate and atomic resolutions. The in situ differential descriptors of the polarized subsystems are emphasized and alternative energy profiles in interactions between hard and soft acidic and basic reactants are used to investigate the process representative activation and reaction energies. The intersecting-state model of such acid-base (AB) systems is explored, its predictions of the reaction transition-state complex and its properties are summarized, and composite (AB)n systems are commented upon.

Introduction

The advent of Density Functional Theory (DFT) [1-6] has brought a renewed interest in molecular electron densities and the associated “population” degrees of freedom as primary descriptors of the mechanism and progress of elementary chemical reactions [7-16]. This also covers the probabilistic models of the chemical bond in Information Theory (IT) [16,17] in all resolution levels of electronic distributions, from the local description of densities themselves to intermediate descriptions of the overall electron numbers in molecular substrates, their active sites or constituent atoms. For example, such “condensed” descriptions may involve occupation numbers of the configuration Molecular Orbitals (MO) or probability data regarding the adopted definition of bonded Atoms-in-Molecules (AIM) or specific basis set of Atomic Orbitals (AO) used in molecular calculations.

The most condensed level, of a global description in terms of the average electron numbers on reactants, requires an identification of the in situ reactivity criteria for an (isoelectronic) charge-transfer (CT) phenomena in the externally-closed reactive system as a whole [9,11,12,16-18], e.g., in the acid (A, acceptor)  base (B, donor) (AB) complexes. A determination of the optimum amount of such “concerted” displacements in overall electron populations and the subsequent equilibrium responses of reactants, involves the reaction chemical potential (gradient) and hardness (Hessian) descriptors. Their known finite-difference estimates, used in qualitative considerations, e.g., [4,9-13,19], ultimately refer to the substrate ionization-potential (I_α) and electron-affinity (A_α) properties. In this work, we reexamine definitions of the proper CT descriptors of the closed and open reactants, all of which can be determined from the canonical data on the system constituent AIM [9,10].

The population reference systems of the substrates have to be mutually oriented in an AIM-resolved reaction mechanism. In the Intersecting-State Model (ISM) [10-12] this has been accomplished by requiring collinearity of the reactant internal Fukui Functions (FF), each reflecting the populational “trajectory” of the most efficient mode of an electron “inflow” or “outflow” to/from the molecular fragment in question. The ISM perspective has also anticipated a lowering of the process activation energy upon an external “opening” of the reactive system in contact with an electron reservoir, e.g., the (macroscopic) catalytic surface. In the present analysis, we shall summarize these conjectures and briefly explore the possibility of supramolecular assemblies of the bonded a_B monomers.

Charge-transfer in reactant resolution

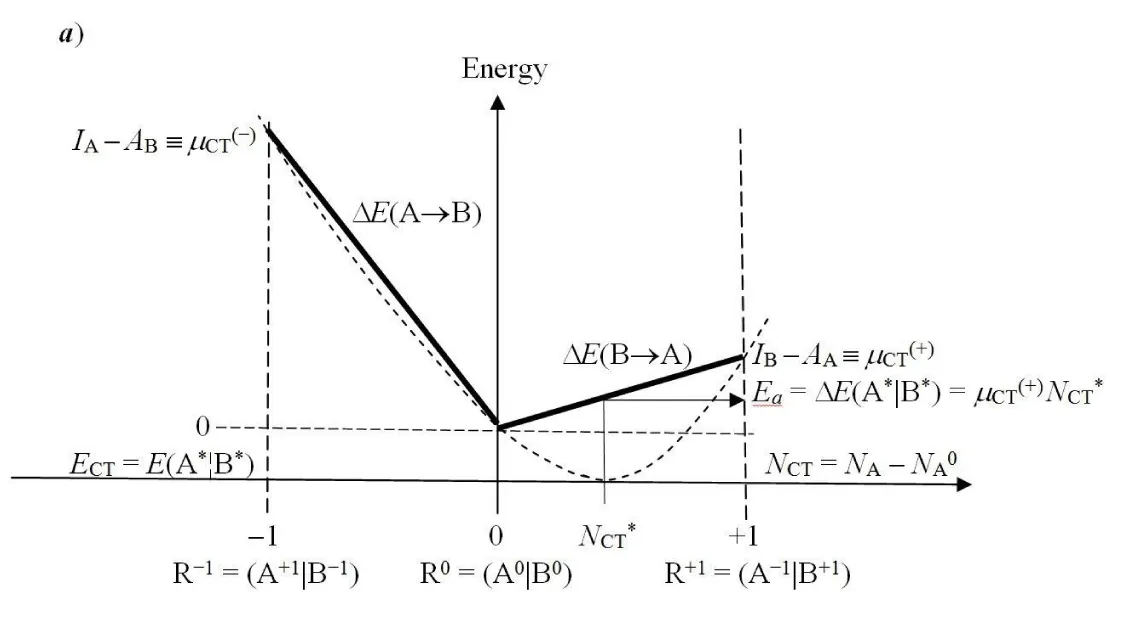
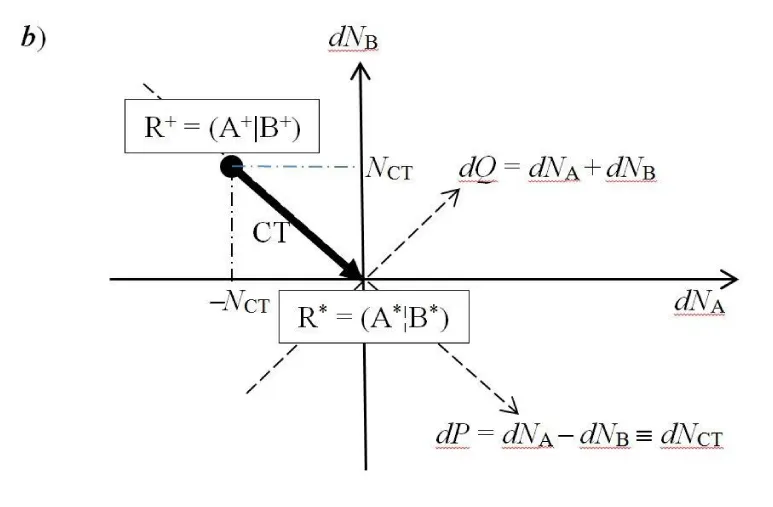
Let us briefly reexamine the populational derivatives characterizing a general CT reactive system R ≡ AB. We aim to describe the internal (isoelectronic) transfer of the equilibrium amount of N_CT electrons between the initially closed reactants in the nonequilibrium (nonbonded) complex R⁺ = (A⁺|B⁺), from the polarized “donor” reactant B+ to its “acceptor” partner A⁺,

dN_A = −dN_B = N_CT > 0 or dN_R ≡ dN_A + dN_B = 0, (1)

for the fixed molecular external potential v(r) = v_A(r) + v_B(r), corresponding to the “frozen” geometry of R as a whole. The optimum CT flow ultimately produces the equilibrium (bonded) complex R* = (A*¦B*) (Figure 1). The vertical solid and broken lines in R⁺ and R*, respectively, symbolize the “barrier” and “freedom” to exchange electrons between the externally-closed reactants [9-12]. For simplicity, we further assume that internal geometries of the isolated reactants A0 and B0 are held frozen in the reaction complex, so that there exists a unique “molecular” reference R0 ≡ (A0|B0), consisting of the free reactants shifted to their current mutual orientation and separation in R. Again, the vertical solid line separating the nonbonded fragments of R0 implies that they both conserve their initial electron numbers, when polarized by a presence of the other subsystem: N_α0 = N_α⁺, α = A, B.

Such an internal transfer of N_CT electrons in R*, between the already polarized reactants of R⁺ ≡ (A⁺|B⁺), thus conserves the complex overall number of electrons: N_A ⁺ N_B ≡ N_R. The equilibrium electron populations on subsystems, N* = (N_A*, N_B*), which directly result from integrations of the associated fragment densities ρ* = (ρA*, ρB*),

N_α* = ∫_ρα*(r) dr, α = A, B;

N* ≡ N⁰ + ∆N*(N_CT) = (N_A* = N_A⁰ + N_CT, N_B* = N_B⁰ − N_CT), (2)

Ultimately determine the optimum amount of the B→A CT:

N_CT = N_A* − N_A⁰ = N_B⁰ − N_B* > 0 or ∆N*(N_CT) = N_CT (1, −1). (3)

Here, the row vector N⁰ = (N_A⁰, N_B⁰) groups the electron populations of the reference (free or polarized) reactants in non-bonded complexes R0 or R+.

The equilibrium densities ρ+(N_R⁺) and energies E+(N_R⁺) of the externally open but mutually closed reactants in the composite macroscopic system involving separate electron reservoirs for each substrate, M+ ≡ (RA¦A⁺|B⁺¦RB), thus depend on their current (average) electron populations N_R⁺ = {N_α⁺} (“row” vector), giving rise to overall (average) electron number in R⁺as a whole: N_R⁺ = ∑_α N_α⁺. These functions ultimately determine charge sensitivities of the “embedded”, polarized reactants {α⁺}, including the (row vector) of the chemical potentials in polarized subsystems,

μ_R⁺ = ∂E+(N_R⁺)/∂N_R⁺ = {µ_α = ∂E⁺(N_R⁺)/∂N_α⁺}, (4)

and the hardness matrix in this reactant resolution:

η_R⁺ = ∂²E⁺(N_R⁺)/∂N_R⁺ ∂N_R⁺ = {ηα,β = ∂²E⁺(N_R⁺)/∂N_α+ ∂N_β+ = ∂µβ+/∂N_α+}. (5)

In this “condensed” resolution the overall fragment populations N_R = (N_A, N_B) = {N_α} represent the system independent electronic-structure variables, which determine the populational derivatives of reactants: their chemical potentials μ_R = ∂E_R(N_R)/∂N_R = {µ_α} and hardness matrix η_R = ∂²E^R(N_R)/∂N_R ∂N_R = ∂μR/∂N_R = {η_α,β}. The fragment populations combine into the normal coordinates describing R as a whole: polarization, P = N_A − N_B, and CT, Q = N_A + N_B ≡ N_R. In such a collective representation the system internal (isoelectronic) CT is thus directed along the polarization coordinate P, by the population shift N_CT = (N_CT, −N_CT) of the “closed-to-open” transition R⁺ ≡ (A⁺|B⁺) .→ R* ≡ (A*¦B*), which corresponds to the vanishing external-CT displacement: dQ = 0. This CT process results in stabilization energy ∆E(NCT) ≡ ECT < 0 and requires the population-activation of the mutually-closed (equilibrium) subsystems: ∆E(A^a|B^a) ≡ E_a = E(A*|B*) − E(A⁺|B⁺) = µ_CT⁽⁺⁾ N_CT* > 0. In Panel C the reaction energy profile along the CT coordinate x consists of the “basis-activation” curve, E_B^R(x) = − µ_B x + ½η_B^R x², for 0 ≤ x ≤ N_CT, followed by the “acid-stabilization” function, E_A^R(x) = µ_A x + ½η_A^R x², for N_CT ≤ x ≤ 2N_CT, with a common value E_A^R(x^‡) E_B^R(x^‡) ≡ E_a = E(A*|B*) in the transition-state (TS) at x^‡ = N_CT. These two energy segments are juxtaposed in Panel d as functions of the CT-progress variable y ∈ [0, NCT]. Their intersection determines the representative amount of CT “activation”, 0 ≤ y^‡ ≡ N_CT ≤ N_CT, and the associated energy: E_a = E_A^R(y^‡) = E_B^R(y^‡).

These condensed descriptors define the associated second-order expansion of electronic energy in terms of powers of displacements in overall populations on subsystems,

∆E⁺(∆N_R⁺) = ∆N_R⁺ (∂E⁺/∂N_R⁺) + ½ ∆N_R⁺ [∂2E⁺/∂N_R⁺ ∂N_R⁺] ∆N_R⁺,T

= ∆N_R⁺ μ_R⁺,T + ½ ∆N_R⁺ η_R⁺ ∆N_R⁺,T. (6)

In the fixed (molecular) external potential v(r) of the Born-Oppenheimer (BO) approximation, for the equilibrium amount N_CT of CT in R*(N_CT), NR(N_CT) = {N_α*(N_CT)}, a similar population-dependence characterizes the electron densities and energy of the mutually-open (bonded) reactants, in the composite macroscopic system involving a common electron reservoir for both substrates, M* ≡ (R¦A*¦B*) = (R¦R*),

ρ*[N_R(N_CT); v] = ρ_R(N_CT), E*[N_R(N_CT); v] = E_R[N_R(N_CT)] ≡ E(N_CT). (7)

The equilibrium amount of CT thus represents the reaction coordinate, a progress variable in such internal displacements of the system's electronic structure. The associated in situ descriptors then involve differentiations concerning this amount of B→A CT [9-12,16-18]. The closure relation of Eq. (1) implies the following populational derivatives of reactants along this internal CT coordinate, generating the row-vector of their FF indices

F_R^CT = ∂N_R/∂N_CT = (F_A^CT, F_B^CT), ∑_α F_α^CT = 0;

F_A^CT = ∂N_A⁺(N_CT)/∂N_CT = 1 and F_BCT = ∂N_B⁺(N_CT)/∂N_CT = −1. (8)

These “condensed” subsystem indices enter as “weighting” factors into the chain-rule expressions for the relevant in situ CT descriptors. For example, the CT chemical-potential displacement, the energy-conjugate of N_CT,

µ_R^CT = ∂E(N_CT)/∂N_CT = ∑_α (∂N_α+/∂N_CT) (∂E+/∂N_α+)

= ∑_α F_α^CT µ_α = F_R^CT μ_R^+,T

= F_A^CT [∂E⁺(N_R)/∂N_A] + F_B^CT [∂E+(N_R)/∂N_B] = µ_A − µ_B, (9)

measures the initial difference of chemical potentials in the “embedded” (polarized) subsystems of R+ and represents the driving force for the subsequent bond-formation process. The associated CT-hardness measure similarly reads:

η_R^CT = ∂²E(N_CT)/(N_CT)² = ∑_α ∑_β (∂N_α⁺/N_CT) (∂²E⁺/∂N_α⁺ ∂N_β⁺) (∂N_β⁺/N_CT)

= ∑_α ∑_β F_α^CT η_α,β F^CT = F_R^CT η_R⁺ F_R^CT,T

= (η_A,A − η_A,B) + (η_B,B − η_B,A) ≡ η_A^R + η_B^R. (10)

Here, η_α^R denotes the effective hardness of the “embedded” fragment α⁺ in R⁺. Thus, at finite separations, the hardness descriptors of chemically interacting reactants, reflecting the presence of complementary subsystem β≠α (a finite electron “reservoir”), which effectively softens the fragment α, are modified by a finite off-diagonal hardness

η_β,α = ∂²E+(N_R⁺)/∂N_β+ ∂N_α+ = ∂µ_α+(N_R⁺)/∂N_β+.

The in situ CT-softness descriptor is then accordingly defined as the inverse of the above global CT-hardness index:

S_R^CT = ∂N_CT/∂µ_CT = ∂N_B^CT/∂µ_CT = − NBCT/∂µ_R^CT = 1/η_R^CT. (11)

These combined descriptors ultimately determine the associated 2nd-order change in electronic energy, ∆E(N_CT), due to the internal displacement in the Donor-Acceptor (DA) reactive system R = AB,

∆E(N_CT) = µ_R^CT N_CT + ½ η_R^CT(N_CT)²

= [µ_A N_CT + ½η_A^R (N_CT)²] + [−µ_B N_CT + ½η_B^R (N_CT)²] ≡ ∑_α ∆E_α(N_CT), (12)

the sum of reactant contributions {∆E_α(N_CT)}.

The equilibrium condition, of the vanishing CT gradient of electronic energy at R*,

∂E(N_CT)/∂N_CT|* = µ_R^CT(N_CT*) ≡ µ_A(N_CT*) − µ_B(N_CT*) = µ_R^CT +η_R^CT N_CT* = 0, (13)

then yields the optimum amount N_CT* of CT (Figure 1a),

Figure 1: The internal CT process in a reactive system R = A-B combines the acceptor (acid, A) and donor (base, B) substrates. Panel a: chemical potential discontinuity and the system CT activation; Panel b: displacements in subsystem populations and normal modes for charge reorganizations in the open system; Panel c: energy profile for the bond-formation reaction along the isoelectronic (N-restricted) CT process (A+|B+) → (A*|B*) → (A*¦B*); Panel d: juxtaposed energy plots for the “basis-activation” and “acid-stabilization” along the progress variable y measuring the current amount of B→A CT; Panel e: transition-state analysis of the Hard (H) and Soft (S) acids and bases.

N_CT* = −µ_R^CT/η_R^CT > 0, (14a)

∆E(N_CT*) ≡ E_CT(N_CT*) − E_CT(N_CT = 0) = − ½ (µ_R^CT)2/η_R^CT ≡ E_CT, (14b)

for which the chemical potentials of both reactants equalize at the molecular level

µ_R = ∑_α (∂E_R/∂N_α) (∂N_α/∂N_R) ≡ ∑_α µ_α f = µA (η_B^R/ηCT) + µ_B (η_A^R/η_CT)

= µ_A* = µ_A + η_A^R N_CT* ≡ µ_A(N_CT*)

= µ_B* = µ_B − η_B^R N_CT* ≡ µ_B(N_CT*). (15)

The CT activation energy E_a of Figure 1a is determined by the equilibrium population shifts in the mutually closed, population-activated reactants {α^a} in contact with their respective reservoirs: N_A* = N_A⁰ + N_CT* and N_B* = N_B⁰ − N_CT*. These displacements are effected by appropriate exchanges with the separate (macroscopic) reservoirs of subsystems in the composite polarized system M+ ≡ (R_A¦A+|B+¦R_B):

E_a = E(A*|B*) − E(A+|B+) ≡ ∆E(A^a|B^a). (16)

Summing the energy changes of such populationally-activated subsystems in the B→A CT then gives:

E_a = ∆E(A^a) + ∆E(B^a) = [µ_A+ N_CT* + µ_B+ (N_CT*)]

= (I_B − A_A) N_CT* ≡ µ_CT⁽⁺⁾ N_CT* > 0, (17)

where A_α and I_α stand for the electron affinity and ionization potential of reactant α, respectively, while

µ_CT⁽⁺⁾ = I_B − A_A = µ_CT(B→A) > 0 (18)

denotes the biased chemical-potential difference [16] for the “positive” B→A CT in Figure 1a. It should be recalled, that the chemical potential µ_α in Eq. (9) represents the unbiased descriptor of chemical species, when we have no information about its action in the reactive complex.

In Mulliken’s (M) interpolation [19] it is expressed by the arithmetic average of the system acidic (anionic, acceptor), α(−) = −Iα, and basic (cationic, donor), µ_α(+) = −Aα, measures,

µ_α^(M)= ½ [µ_α(−) + µ_α(+)] = − ½ (Iα + A). (19)

Therefore, in this finite-difference estimate (Figure 1a)

µ_CT^(M) = µ_A^(M) − µ_B^(M) = ½ [µ_CT⁽⁺⁾ − µ_CT⁽⁻⁾], (20)

where the biased chemical-potential difference for the (“negative”) A→B CT in Figure 1a

µ_CT⁽⁻⁾ = I_A − a_B ≡ µ_CT(A→B) > 0. (21)

The biased measures reflect the (macroscopic) chemical-potential discontinuity [20].

The “weighting” factors of the substrate chemical potentials μR+ = {µ_α} in the combination-rule of Eq. (15) represent the external FF indices in R,

f_R = {f_A = ∂N_A/∂N_R = η_B^R/η_CT, f_B = N_B/∂N_R = η_A^R/η_CT}, (22)

measuring responses in populations of complementary subsystems to an inflow (dN = dN_R 0) or outflow (dN = −dN_R < 0) of electrons to/from the equilibrium complex R* = (A*¦B*). The global hardness of R* as a whole, η_R = ∂²E^R(N_R)/∂N_R², similarly reflects the external NR-derivative of the system resultant chemical potential,

η_R = ∂µ_R/∂N_R = ∑_β ∑_α (∂N_β/∂N_R) (∂µ_α/∂N_β) f_α = ∑_β ∑_α f_β η_β,α f_α

= (η_A,Aη_B,B − η_A,Bη_B,A)/η_R^CT ≡ D(η_R⁺)/η_R^CT, (23)

where D(η_R⁺) stands for the determinant of the hardness matrix η_R⁺. The inverse of this population-Hessian measures the global softness of R*:

S_R = ∂N_R/∂µ_R = η_R^CT/D(η_R⁺). (24)

Let us now examine in more detail the alternative indices of the relative-softness (FF) quantities in the DA reactive complex R = A-B. One observes that derivatives of Eq. (8) represent the overall FF indices of reactants for an isoelectronic (internal) CT, in an externally-closed R. This conservation of the overall number of electrons is indeed reflected by their vanishing sum:

F_A^CT + F_B^CT = (∂N_R/∂N_CT)_N = 0. (25)

The “condensed” descriptors of reactants result from an integration of the associated “local” FF in substrate resolution, f^CT(r) = {f_α^CT(r) = ∂N_α/∂N_CT},

∫f_A^CT(r) dr = ∂N_A/∂N_CT = F_A^CT, ∫f_B^CT(r) dr = ∂N_B/∂N_CT = F_B^CT.

The latter also follow the appropriate chain rules:

f_A^CT(r) = ∂_ρA(r)/∂N_CT = ∑_α [∂_ρA(r)/∂N_α] F_α^CT

= ∂_ρA(r)/∂N_A − ∂_ρA(r)/∂N_B ≡ f_A,A(r) − f_B,A(r), (26)

f_B^CT(r) = ∂_ρB(r)/∂N_CT = ∑_α [∂_ρB(r)/∂N_α] F_α^CT

= ∂_ρB(r)/∂N_A − ∂_ρB(r)/∂N_B ≡ f_A,B(r) − f_B,B(r). (27)

These local responses on reactants give rise to the overall in situ FF of R as a whole:

f_R^CT(r) = ∂_ρR(r)/∂N_CT = ∂_ρA(r)/∂N_CT + ∂_ρB(r)/∂N_CT = f_A^CT(r) + f_B^CT(r),

∫f_R^CT(r) dr = F_A^CT + F_B^CT = 0. (28)

To conclude this section, let us briefly summarize the softness and FF indices of the (nonbonded) composite reactive system R⁺ = (A+|B+), expressed in terms of elements in η_R⁺. The inverse of the “condensed” hardness matrix, η_R⁺ = {η_α,β}, α, β ∈ (A, B), which determines the determinant D(η_R⁺) = η_A,Aη_B,B − η_A,Bη_B,A ≡ D, ultimately defines the softness matrix

σ_R⁺ = ∂N_R⁺/∂μ_R⁺ = (η_R⁺)⁻¹ = {S_α,β},

S_A,A = η_B,B/D S_A,B = −η_B,A/D

S_B,A = −η_A,B/D S_B,B = η_A,A/D , (29)

grouping the chemical potential derivatives of the grand-potential

Ω+(μ_R⁺) = E⁺(N_R) − μ_R⁺N_R.

It further generates the associated fragment and global response descriptors. For example, the softnesses of the bonded (embedded) subsystems in R* = (A*¦B*),

S_A^R = (η_B,B −η_A,B)/D ≡ η_B^R/D, S_B^R = (η_A,A −η_A,B)/D ≡ η_A^R/D, (30)

generate the additive contributions to the global softness S_R of the whole R, the inverse of the global hardness η_R,

S_R = S_A^R + S_B^R = (η_A^R + η_B^R)/D = η_R^CT/D = η^R−1, (31)

and the condensed FF indices of reactants:

f_A^R = ∂N_A/∂N = S_A^R/S_R = η_B^R/η_R^CT

and f_B^R = ∂N_B/∂N = S_B^R/S_R = η_A^R/η_R^CT. (32)

Therefore, the resultant hardness of R as a whole can be directly expressed in terms of elements of the condensed hardness matrix in reactant resolution:

η_R = 1/S_R = D/η_R^CT = (η_A,Aη_B,B − η_A,Bη_B,A)/(η_A,A + η_B,B − 2η_A,B). (33)

The fractional populations of subsystems, and the average numbers of electrons on molecular fragments, require an ensemble description [21]. Indeed, the external inflow or outflow of electrons must involve a macroscopic electron reservoir, while in the internal exchanges in R one substrate acts as a microscopic “reservoir” to its reaction partner [16]. Contrary to the external discontinuity of the chemical potential in a molecular reactive system coupled to the external reservoir (Figure 1a) [20], the in situ electronegativity difference, which drives electron flows between the microscopic (externally closed) reactants, represents the continuous function of the fractional amount of CT: E_R = E(N_CT) [16]. This validates Mulliken’s [19] parabolic interpolation and confirms it as a genuine energy function in an internal ensemble description.

In the ensemble approach to R+ one refers to the externally open but mutually closed (chemically nonbonded) reactants in the composite macroscopic system M+ ≡ (RA¦A+|B+¦RB) involving separate electron reservoirs for each polarized substrate. The equilibrium shifts in subsystem populations, ∆N_R⁺ = {N_α}, then respond to displacements in the reservoir chemical potentials ∆μ_R⁺ ={∆µ_α}:

∆N_R⁺ = ∆μ_R⁺ σ_R⁺ or μ_R⁺ = ∆N_R⁺ η_R⁺. (34)

The hardness (η_R⁺) and softness (σ_R⁺) matrices thus relate the equilibrium “displacements” in the reservoir chemical potentials, equal to the corresponding descriptors of reactants, with the conjugate “responses” in fragment electron populations.

The DA system R(x) = A^R(x)  B^R(x), where x measures the current amount of the B→A CT, can be also viewed as a prototype of the bond-formation reaction between the initially non-bonded (polarized) reactants (Figure 1c):

(A⁺|B⁺) → (A*|B*) → (A*¦B*). (35)

The energy profile of this CT reaction is then derived from the resultant expression for the energy [see Eqs. (12) and (14b)]:

∆E(x) = µ_R^CT x + ½ η_R^CTx² = (µ_A x + ½η_A^R x²) + (−µ_B x + ½η_B^R x²) ≡ E_A^R(x) + E_B^R(x)

= [(µ_A x + ½η_A,A x²) + (−µ_B x + ½η_B,B x²)] − 2η_A,B x² ≡ [E_A(x) + E_B(x)] + E_AB(x). (36)

It is seen to combine contributions due to the embedded reactants in R: the “base-activation” curve E_B^R(x) and the “acid-stabilization” function E_A^R(x), with the “transition state” (TS) complex R^‡ = (A*|B*) for x^‡ = N_CT composed of the closed (nonbonded) equilibrium reactants {α*}, simultaneously population-activated. Sitting next to the zero-energy at the initial polarized complex for x = 0, E(A⁺|B⁺) ≡ 0, then identifies the reaction energy as that corresponding to the bonded, mutually-open reactants (Figure 1a):

E_r = E(A*¦B*) = ECT. (37)

For a finite x, the in situ energy of CT complex has been alternatively partitioned in Eq. (36) into the uncoupled-reactant contributions {E_α(x) > 0} describing the {α⁺→α(x)} transitions, and the interaction energy:

E_AB(x) = − 2η_A,B x² < 0. (38)

The latter stabilizes the reactive complex since the coupling hardness reflects the Coulomb repulsion between electrons on both fragments: η_A,B ≈ γ_A,B > 0.

The typical energy profile for this bond-formation process (Figure 1c) can be viewed as consisting of the base-activation segment E_B^R(x), for 0 ≤ x ≤ N_CT, and the acid-stabilization part E_A^R(x), for N_CT ≤ x ≤ 2NCT, with the activation energy at the intersection point x‡ = NCT:

E_A^R(x^‡) = E_B^R(x^‡) ≡ E_a > 0. (39)

Alternatively, these two segments can be juxtaposed along a common CT-progress variable y ∈ (0, N_CT) measuring the current amount of the B→A CT (Figure 1d) [10-12]. The intersection y‡ of the energy plots E_B^R(y) and E_A^R(y),

E_A^R(y^‡) = E_B^R(y^‡) ≡ E_a, (40)

then determines yet another representative position y^‡ ≡ N_CT and activation energy E_a for the isoelectronic CT in a_B systems. This representation facilitates a discussion of “dynamical” aspects of the Hard(H)−Soft(S) Acids(A) and Bases(B) (HSAB) principle of chemistry (Figure 1e) [7,10-12,22-26]. One recalls, that the opposite-hardness combinations H−S and S−H have been identified as producing relatively unstable complexes, with the comparable-hardness compounds H−H and S−S acquiring their relative stability due to stronger inter-substrate chemical bonds: covalent in S−S complex [7] and ionic in H−H compound [23]. Indeed, the largest values of CT-amount should characterize the covalent, S-S structure, the mixed-hardness species are predicted to exhibit moderate values of N_CT, while its lowest value can be expected in the ionic, H-H structures. A reference to Figure 1e shows that all these hardness combinations generate a cluster of similar energies {E_a} and corresponding CT measures {N_CT}, predicting an “early” position of a “low” activation barrier. Specific orderings in these predictions should depend strongly on the actual combinations of reactant harnesses (compare [10,11,12]).

Atomic resolution of electronic reorganizations and intersecting-state model

For some interpretations in chemistry the preceding “condensed” perspective, in which reactants are viewed as whole units, may require a more detailed resolution, e.g., in terms of the (bonded) constituent AIM, the system occupied MO or the AO basis functions of molecular calculations.

Consider the illustrative case of atomic approach to the DA reactive system R, with the row vectors N_A = {N_a} and N_B = {N_b} now grouping the average AIM populations in both substrates, ∑_a N_a = N_A and ∑_b N_b = N_B, for the fixed external potential v(r) = v_A(r) + v_B(r) due to the rigid molecular geometry. They combine into the overall population (row) vector in atomic resolution, N^R = (N_A, N_B), with the system electronic energy being now regarded as its function: E^R(N^R) = E^R({N_α}). This selection of electronic variables in turn determines the associated differential descriptors: the row vector of atomic chemical potentials,

u^R = ∂E^R/∂N^R = (u_A, u_B) = {u_α = ∂E(N^R)/∂N_α}, (41)

and the square hardness matrix in atomic resolution:

h^R = ∂²E^R/∂N^R ∂N^R = ∂u^R/∂N = {∂u/∂N_α ≡ h_α,β = h_β,T ≡ [∂uα/∂N_β]T}. (42)

The latter ultimately determines the AIM softness descriptors:

s^R = (h^R)^-1 = ∂N^R/∂u^R = {s_β,α = ∂N_α/∂u_β}. (43)

This softness matrix now transforms the resolution chemical-potential displacements u^R into the conjugate populational responses ∆N^R:

∆N^R = ∆u^R s^R or ∆u^R = ∆N^R h^R. (44)

The second-order change in electronic energy due to populational displacements ∆N^R of AIM then reads:

∆E(∆N^R) = ∆N^R u^R,T + ½ ∆N^R h^R ∆N^R,T ≡ ∆E⁽¹⁾(∆N^R) + ∆E⁽²⁾(∆N^R). (45)

Its quadratic term

∆E⁽²⁾(∆N^R) = ½ ∑_α ∑_β ∆N_α h_α,β ∆N_βT ≡ ∑_α ∑_β ∆E⁽²⁾(α, β), (46)

defines in atomic resolution the energy paraboloid of the CT reactive system. It contains the (diagonal) intra-reactant surfaces (Figure 2),

Figure 2: Population activation (A+B+) → (A*|B*) of the initially polarized (mutually-closed) reactants {α+}, each exhibiting two internal (populational) degrees-of-freedom, N_A ={N_a, N_a’} and N_B = {N_b, N_b’}. This displacement of the average populations in subsystems, N_A = N_a + N_a’ and N_B = N_b + N_b’, respectively, is effected in the externally open composite system (R_A¦A+|B+¦R_B), which involves a separate reservoir for each subsystem. In the isoelectronic CT process, when dN_A + dN_B = 0, the displaced substrate populations, dNA = N_CT and dN_B = −N_CT, correspond to a common direction of the reactant internal FF {f_α = ∂N_α/∂N_α}. This convention mutually orients both the AIM population spaces {N_α} of subsystems and their energy paraboloids {E_α+(N_α) = ½∑_i∈α∑_j∈α dN_i^α η_i,j_α dN_j^α = ½ [hP_α (dN_P^α)2 + h_Q^α (dN_Q^α)2]}, determined by the (diagonal) reactant blocks h_α,α of the system overall hardness matrix in atomic resolution: h^R = {h_α,β}; here P_α and Q_α respectively denote the “polarization” and “charge-transfer” (CT) normal modes of reactant α⁺, polarized in presence of its molecular partner.

E_α+(∆N_α) ≡ ∆E⁽²⁾(α,α) = ½ ∆N_α h_α,α’ ∆N_α’T = ½ ∑_a∑_a’ N_a h_a,a’ ∆N_a’, α = A, B; (47a)

and the (off-diagonal) interaction contribution for α ≠ β

∆E⁽²⁾(α, β) + ∆E⁽²⁾(β, α) = ∑_a∈α∑_b∈β ∆N_a h_a,b ∆N_b. (47b)

These canonical descriptors of AIM in R = a_B can be also combined into the global reactant properties of the preceding section, and ultimately into those describing R as a whole. This is effected by weighting them into the average descriptors using the appropriate set of (atomic) FF indices:

G^R = ∂N^R/∂N_R = {g_α = ∂N^R/∂N_α}. (48)

The chain-rule transformation of derivatives provides the required combination rules:

µ_α = ∂E⁺(NR)/∂N_α = ∂E^R(N^R)/∂N_α = (∂N^R/∂N_α) (∂E^R/∂N^R) ≡ g_α u^R,T

= ∑_β (∂N_β/∂N_α) (∂ER/∂N_β) ≡ ∑_β g_α,β uβ T or μR+ = GR uR,T; (49)

η_α,β = ∂²E⁺(N_R)/∂N_α ∂N_β = = ∂²E^R(NR)/∂N_α ∂N_β

= (∂N^R/∂N_α) (∂²E^R/∂N_R ∂N_R) (∂N_R/∂N_β) = g_α h_R g_β^T

= ∑_γ∑_δ (∂N_γ/∂N_α) (∂²E^R/∂N_γ ∂N_δ) (∂N_δ/∂N_β) ≡ ∑_γ∑_δ G_α,γ h_γ,δ G_δ,α^T or

η_R⁺ = G^R h^R G^R,T. (50)

Here, the combined matrix of internal FF descriptors of constituent atoms in both reactants reads

G_A,A = ∂N_A/∂N_A, G_A,B = ∂N_B/∂N_A

G_B,A = ∂N_A/∂N_B, G_B,B = ∂N_B/∂N_B (51)

and the external FF indices F^R = ∂N^R/∂N_R group the populational responses of AIM to an inflow or outflow dN_R of electrons to/from R as a whole:

F^R = ∂N^R/∂N_R = (F_A^R = ∂N_A/N_R, F_B^R = ∂N_B/∂N_R). (52)

The diagonal blocks in G^R define the internal FF of AIM in each separate reactant (Figures 2,3):

Figure 3: Moderating effect of the reactant external-opening in the composite system M+ ≡ (R_A¦A+|B+¦R_B) upon the activation energy of CT systems: E_a^restricted > E_a^unrestricted.

G_A,A = ∂N_A/∂N_A ≡ f_A = {f_a = ∂N_a/∂N_A} and

G_B,B = ∂N_B/∂N_B ≡ f_B = {f_b = ∂N_b/∂N_B}. (53)

The resultant chemical potential and hardness of the whole reactive complex are given by the appropriate FF-weighted, external averages of AIM descriptors:

µ_R = ∂E^R/∂N_R = (∂N^R/N_R) (∂E^R/∂N^R) = F^R u^R,T

= ∑_α (∂N_α/∂N_R) (∂E^R/∂N_α) = ∑_α F_α^R u_α^T, (54)

η_R = ∂²E_R/∂N_R² = (∂N^R/∂N_R) (∂²E^R/∂N^R∂N^R) (∂N^R/∂N_R) = F^R h^R F^R,T

= ∑_α ∑_β (∂N_α/∂N_R) (∂²E^R/∂N_α ∂N_β) (∂N_β/∂N_R) = ∑_α ∑_β F_α^R h_α,β F_β^R,T. (55)

The atomic resolution of electronic structure offers chemically interesting details of molecular rearrangements in chemical reactions. They cover descriptors of both the “internal”, N-restricted process of the bond-formation between reactants and the “external”, N-unrestricted effects, due to the intervention of an electronic reservoir. A reference to Figure 3 indeed suggests, that such an “opening” of the reactive system in the N-unrestricted CT should lower the required activation energy (see also [10-12]).

When combining reactant paraboloids in ISM one ultimately encounters the problem of the unique mutual orientation of the AIM population spaces in both reactants. The natural choice is dictated by the requirement that the reactant FF vectors of Eq. (53) are collinear in the isoelectronic, N-restricted CT processes in DA systems. Indeed, electrons removed from the basic subsystem, most efficiently along the f_B direction, are subsequently donated to the acidic subsystem, most effectively along the f_A vector. This convention is adopted in Figures 2,3.

The N-unrestricted mechanism deviates from this collinearity (Figure 3). It can be realized in catalytic systems, where the surface active sites provide electron reservoirs for chemisorbed reactants. A reference to Figure 3 also shows that this external opening of reactants may have a moderating effect on their activation in CT processes. The “softening” influence of the system environment should thus constitute an important factor in the catalytic activity of heterogeneous systems.

The Mulliken-type formulas [4,10,16,19],

u_k ≈ − ½ [I_k + A_k] ≡ u_k^(M), h_k,k ≈ Isub>k − Asub>k ≡ h_k,k^(M), h_k,l ≈ ½[h_k,k + h_l,l] ≡ h_k,l^(M), (56)

approximate the canonical AIM data of Eqs. (41) and (42). The off-diagonal hardnesses in h^R = {h_k,l = ∂²E^R/∂N_k ∂N_l = ∂u_l/∂N_k}, can be then “scaled” geometrically,

h_k,l ≈ h_k,l(M) S_k,l(R_k,l), (57)

where S_k,l stands for the overlap integral S_k,l = 〈s_k|s_l〉 between the representative s-type orbitals in the valence shells of atoms k and l. This representation separates the “property” descriptor h_k,l^(M) from its geometrical factor S_k,l(R_k,l), depending on the inter-atomic distance R_k,l. It correctly reproduces the diagonal atomic descriptor, for k = l and hence S_k,k(R_k,k=0) = 1, and predicts the vanishing population coupling at large distances: S_k,l(R_k,l→∞) = 0. This estimate of the coupling hardness also satisfies the Maxwell cross-differentiation identity: h_k,l = h_l,k. Such finite-difference data can be ultimately transformed into the reactant descriptors of Eqs. (49) and (50).

Alternatively, the interpolations of the valence-shell electron-repulsion integrals, familiar from the semi-empirical LCAO MO theories, e.g., the Mataga-Nishimoto or Ohno formulas, can be used to approximate the hardness tensor in atomic resolution [10,27].

The finite-difference measures of the fragment chemical potentials {µ_α^(M) = (I_α + A_α)/2} and hardnesses {η_α^(M) = I_α − A_α} of mono-atomic reactants, A = k and B = l, generate the following in situ descriptors for the “positive” B→A CT, consistent with chemical functions of both substrates in reactive complex (Figure 1a):

µ_R^CT ≈ µ_A^(M) − µ_B^(M) = ½ [(I_B +a A_B) − (I_A + A_A)]

= ½ [(I_B − A_A) − (I_A − A_B)] = ½ [µ_CT⁽⁺⁾ − µ_CT⁽⁻⁾] < 0, (58)

η_R^CT ≈ η_A,A^(M) + η_B,B^(M) − 2η_A,B^(M)

= [(I_B − A_A) + (I_A − A_B)] (1 − S_A,_B) = [µ_CT⁽⁺⁾ + µ_CT⁽⁻⁾] (1 − S_A,_B) > 0, (59)

N_R^CT = − µ_R^CT/η_R^CT = [µ_CT⁽⁻⁾ − µ_CT⁽⁺⁾]/{2[µ_CT⁽⁺⁾ + µ_CT⁽⁻⁾] (1 − S_A,_B)} > 0, (60)

E_CT = − ½ (µR^CT)²/ηR^CT = − ½ [µ_CT⁽⁺⁾ − µ_CT⁽⁻⁾]²/{(1 − S_A,B) [µ_CT⁽⁺⁾ + µ_CT⁽⁻⁾]}. (61)

These expressions in terms of the biased chemical potentials for the reverse directions of CT indicate that an increasing overlap between reactants effectively softens the reactive system, thus facilitating a larger CT amount and greater stabilization energy.

Composite structures involving acid-base complexes

This populational perspective on the molecular electronic structure may also involve larger molecular fragments, e.g., the active parts of the acceptor and donor substrates. Let us symbolically separate the geometrically accessible acidic (a) and basic (b) sites in reactants α ∈ (A, B) from their immaterial remainders:

A = (a_A¦…¦b_A) ≡ (a_A¦b_A) and B = (a_B¦…¦b_B) ≡ (a_B¦b_B).

There are two alternative mutual arrangements of such subsystems in the TS complex: the complementary (c) structure R_c (Figure 4), in which the a-site of one reactant faces the b-site of the other substrate, and the regional-HSAB, parallel (p) structure R_p = R_HSAB, when mutually coordinating sites of both reactants are of the like-hardness character [28-30]:

Figure 4: The elementary CT {b_X→a_Y} and polarizational (P) {a_X→b_X} flows of electrons involving acidic A ≡ (a_A¦b_A) and basic B (a_B¦b_B) reactants in the complementary arrangement Rc of their acidic (a) and basic (b) sites in the reactive complex. These shifts are seen to produce the concerted (“circular”) pattern of electronic fluxes in the final, equilibrium reactive system R_c* = (A*¦B*) = (a_A¦b_A¦a_B¦b_B), when all fragments are free to exchange electrons.

${\text{R}}_c^{}\equiv \left[\begin{array}{c}{a}_{\text{A}}-b_{\text{B}}\\ b_{\text{A}}-a_{\text{B}}\end{array}\right]{\text{ and R}}_{\text{HSAB}}\equiv \left[\begin{array}{c}{a}_{\text{A}}-a_{\text{B}}\\ b_{\text{A}}-b_{\text{B}}\end{array}\right]\equiv {\text{R}}_p.\text{ (62)}$

The acidic (acceptor) site is relatively harder, i.e., less sensitive to an external perturbation, thus exhibiting lower values of the fragment FF index or the associated chemical-softness descriptor, while the basic (donor) fragment is more polarizable, as indeed reflected by its higher response properties. The acidic part in X exerts an electron-accepting (stabilizing) influence on the neighboring fragment of the other reactant Y, while the basic site of X produces an electron-donor (destabilizing) effect on the coordinated region of Y in its vicinity. The purely electrostatic, “ionic” interactions a_A-b_B and a_B-b_A then allow one to predict R_c as the expected preferred structure, while the “covalent” interactions a_A-a_B and b_B-b_A of the HSAB principle point towards Rp as the most stable system. Numerical calculations [28] confirm that complementary interactions of Figure 4, between the electron-rich (basic) fragment of one reactant and the electron-deficient (acidic) fragment of another substrate, indeed establish the most stable TS complex.

This relative stability of R_c reflects an electrostatic dominance in A-B interactions: a (repulsive) basic fragment of one reactant indeed prefers to face an (attractive) acidic part of the reaction partner. The displacements in reactant external potentials due to the presence of the other substrate trigger the induced polarization flows {PX}, which restore the initially displaced intra-substrate equilibria of isolated species. The inter-reactant CT displacements, after the hypothetical opening of the initially closed, polarized reactants, can be directly inferred from the Electronegativity Equalization (EE) principle [31,32]. The combined networks of P and CT displacements between the TS active sites,

then reveal different patterns of probability fluxes in these two reactive complexes: the “concerted” pattern in R_c and the “disconcerted” flow system in R_p [29,30]. They imply the least population displacements (activation) of both reactants in the former and more exaggerated charge displacements on the crucial a_A and b_B sites of the latter. Indeed, in R_c one observes the flow-through behavior on all four active sites, with small net changes in electron populations on all these fragments, while the charge reconstruction in R_p can be regarded as a transfer of electrons from b_B to a_A through the remaining (intermediate) sites a_B and bA. The concerted flows in R_c, which preclude an exaggerated charge depletion or accumulation, thus correspond to the least-displaced electron populations on all four reaction sites. This activation (promotion) perspective provides an additional physical explanation of the complementary preference.

Compared to the isolated species A⁰ and B⁰, the primary coordination B→A in equilibrium DA system ultimately produces an electron-deficient basic substrate B^+δ ≡ B⁽⁺⁾ and an excess electron population on its acidic partner A^−δ ≡ A⁽⁻⁾:

B→A ≡ [A*¦B*] = A⁽⁻⁾B⁽⁺⁾ ≡ M. (63)

Each of the “displaced” reactants then acquires partially “opposite” external character: A⁽⁻⁾ site exhibits an increased tendency to donate electrons to its environment, while B⁽⁺⁾ becomes an effective electron-acceptor site: a_M = B⁽⁺⁾ and b_M = A⁽⁻⁾. In external interactions between “monomers” {Mi}, the bonded A() part of one unit thus represents an accessible “basic” site for interactions with another a_B complex, while the bonded B⁽⁺⁾ fragment stands for an available “acidic” site. Such secondary, “response” actions may influence how such units (“monomers”) combine into larger, supra-molecular structures (“polymers”).

In the spirit of the maximum complementarity [19], the preferred structure of the dimer D_c = M₂ then involves the following pattern of “secondary” coordinations between bonded reactants of different monomers:

For the trimer Tc = M3 one similarly conjectures the following two alternative structures:

Linear (L),

and Cyclic (C):

In all these associations of the (bonded) Acid-Base complexes the “primary” (internal) coordinations A→B = A⁽⁻⁾B⁽⁺⁾ (in monomers) and the “secondary” (external) actions M_i→M_j (between monomers), are seen to enhance each other.

Conclusion

Electron redistributions in chemical processes, and the associated changes of electronic populations on molecules and their active parts ultimately determine the structural patterns and reactivity trends of reactive systems. Different aspects of a “chemical” behavior may require specific reactivity criteria, all dependent on the current distribution of electrons in molecular systems. They may correspond to both the externally closed and -open conditions, each calling for specific descriptors of interacting substrates and displacements in the system's electronic energy.

In this work, we have explored such populational characteristics of CT processes in A(acceptor)B(donor) systems, in both the substrate and AIM resolution levels. The simple models of CT reactivity and ISM in AIM resolution have been reexamined, and the “biased” and “unbiased” measures of reactant chemical potentials and their differences driving N-restricted CT have been discussed. The implications of their discontinuity in the macroscopic ensemble and continuity in Mulliken’s internal ensemble approach have also been stressed. The FF convention for uniting the AIM population spaces of reactants in ISM has been revisited and model implications for lower activation energies in catalytic systems have been reiterated. We have also tackled the combination rules for the condensed CT-reactivity criteria in terms of the corresponding AIM descriptors.

Typical reactivity concepts have been invoked at both the P and CT reaction stages. A qualitative discussion of the DA complexes and composite systems consisting of a_B monomers has also been given. In a_B interactions a dominance of the molecular complementarity over the regional-HSAB behavior has been emphasized and its implications for predicted (AB)n structures have been explored. It has been stressed, that the “primary” B→A coordination in donor-acceptor complexes “reverses” chemical characters of the acidic and basic reactants, thus having a profound influence on the stable patterns of the “secondary” associations of such a_B monomers. In such “polymer” structures the internal and external coordinations enhance each other.

1. Hohenberg P, Kohn W. Inhomogeneous electron gas. Phys Rev. 1964; 136B:864-871.
2. Kohn W, Sham LJ. Self-consistent equations including exchange and correlation effects. Phys Rev. 1965; 140A:1133-1138.
3. Levy M. Universal variational functionals of electron densities, first-order density matrices, and natural spin-orbitals and solution of the v-representability problem. Proc Natl Acad Sci USA. 1979;76(12):6062-6065.
4. Parr RG, Yang W. Density-functional theory of atoms and molecules. New York: Oxford University Press; 1989.
5. Dreizler RM, Gross EKU. Density functional theory: an approach to the quantum many-body problem. Berlin: Springer; 1990.
6. Nalewajski RF, editor. Density functional theory I-IV: Topics in Current Chemistry 180-183. Heidelberg: Springer-Verlag; 1996.
7. Parr RG, Pearson RG. Absolute hardness: companion parameter to absolute electronegativity. J Am Chem Soc. 1983; 105(24):7512-7516.
8. Parr RG, Yang W. Density functional approach to the frontier-electron theory of chemical reactivity. J Am Chem Soc. 1984; 106(14):4049-4050.
9. Nalewajski RF, Korchowiec J, Michalak A. Reactivity criteria in charge sensitivity analysis. In: Nalewajski RF, editor. Density functional theory IV: Topics in Current Chemistry 183. 1996; 183:25-141.
10. Nalewajski RF, Korchowiec J. Charge sensitivity approach to electronic structure and chemical reactivity. Singapore: World Scientific; 1997.
11. Nalewajski RF. Sensitivity analysis of charge transfer systems: in situ quantities, intersecting-state model and its implications. Int J Quantum Chem. 1994; 49(5):675-703.
12. Nalewajski RF. Charge sensitivity analysis as diagnostic tool for predicting trends in chemical reactivity. In: Dreizler RM, Gross EKU, editors. Proceedings of the NATO ASI on Density Functional Theory (Il Ciocco, 1993). New York: Plenum; 1995; 339-389.
13. Geerlings P, De Proft F, Langenaeker W. Conceptual density functional theory. Chem Rev. 2003 May;103(5):1793-873. doi: 10.1021/cr990029p. PMID: 12744694.
14. Chattaraj PK, editor. Chemical reactivity theory: a density functional view. Boca Raton: CRC Press; 2009.
15. Ghosh SK, Chattaraj PK, editors. Concepts and methods in modern theoretical chemistry: Electronic structure and chemical reactivity. Boca Raton: CRC Press; 2013.
16. Nalewajski RF. Chemical reactivity in quantum mechanics and information theory. Elsevier, New York; 2023.
17. Nalewajski RF. Information theory of molecular systems. Amsterdam: Elsevier; 2006.
18. Ciosłowski J, Mixon ST. Electronegativities in situ, bond hardnesses, and charge-transfer components of bond energies from the topological theory of atoms in molecules. J Am Chem Soc. 1993;115(3):1084-1088.
19. Mulliken RS. A new electronegativity scale: together with data on valence states and on ionization potentials and electron affinities. J Chem Phys. 1934; 2(11):782-793.
20. Perdew JP, Parr RG, Levy M, Balduz JL. Density functional theory for fractional particle number: derivative discontinuities of the energy. Phys Rev Lett. 1982; 49(23):1691-1694.
21. Gyftopoulos EP, Hatsopoulos GN. Quantum-thermodynamic definition of electronegativity. Proc Natl Acad Sci U S A. 1968 Jul;60(3):786-93. doi: 10.1073/pnas.60.3.786. PMID: 16591659; PMCID: PMC225120.
22. Pearson RG. Hard and soft acids and bases. Stroudsburg: Dowden, Hutchinson and Ross; 1973.
23. Nalewajski RF. Electrostatic effects in interactions between hard (soft) acids and bases. J Am Chem Soc. 1984; 106(4):944-945.
24. Chattaraj PK, Lee H, Parr RG. HSAB principle. J Am Chem Soc. 1991; 113(6):1855-1856.
25. Gazquez JL, Mendez F. The hard and soft acids and bases principle: an atoms-in-molecules viewpoint. J Phys Chem. 1994; 98(17):4591-4593.
26. Ayers PW. The physical basis of the hard/soft acid/base principle. Faraday Discuss. 2007; 135:161-190.
27. Nalewajski RF, Korchowiec J, Zhou Z. Molecular hardness and softness parameters and their use in chemistry. Int J Quantum Chem Symp. 1988; 22:349-366.
28. Chandra AK, Michalak A, Nguyen MT, Nalewajski RF. On regional matching of atomic softnesses in chemical reactions: two-reactant charge sensitivity study. J Phys Chem A. 1998; 102(48):10182-10188.
29. Nalewajski RF. Manifestations of the maximum complementarity principle for matching atomic softnesses in model chemisorption systems. Top Catal. 2000; 11:469-485.
30. Nalewajski RF. Understanding electronic structure and chemical reactivity: quantum-information perspective. In: Sousa S, editor. The application of quantum mechanics to the reactivity of molecules. Appl Sci. 2019;9:1262-1292.
31. Sanderson RT. An interpretation of bond lengths and a classification of bonds. Science. 1951; 114: 670-672.
32. Sanderson RT. Chemical bonds and bond energy. 2nd edn. Academic Press, New York. 1976.